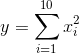当前位置：首页 > 软件库 > 应用工具 > 科研计算工具 >

genetic-algorithm

遗传算法 - Matlab

授权协议 Readme

开发语言

所属分类应用工具、科研计算工具

软件类型开源软件

地区不详

投递者邓星光

操作系统跨平台

开源组织无

适用人群未知

软件概览

遗传算法 - 简书

遗传算法的理论是根据达尔文进化论而设计出来的算法: 人类是朝着好的方向（最优解）进化，进化过程中，会自动选择优良基因，淘汰劣等基因。

遗传算法（英语：genetic algorithm (GA) ）是计算数学中用于解决最佳化的搜索算法，是进化算法的一种。进化算法最初是借鉴了进化生物学中的一些现象而发展起来的，这些现象包括遗传、突变、自然选择、杂交等。

搜索算法的共同特征为：

首先组成一组候选解
依据某些适应性条件测算这些候选解的适应度
根据适应度保留某些候选解，放弃其他候选解
对保留的候选解进行某些操作，生成新的候选解

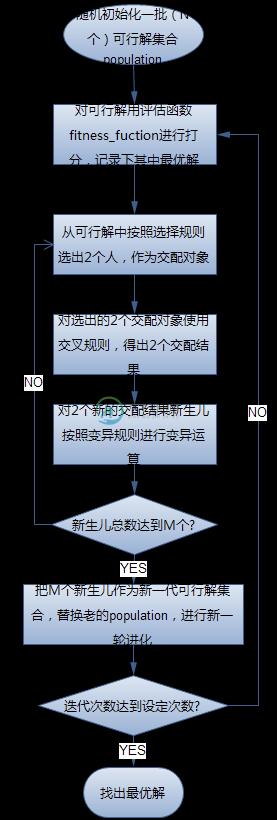
遗传算法的一般步骤

my_fitness函数 评估每条染色体所对应个体的适应度
升序排列适应度评估值，选出 前 parent_number 个 个体作为 待选 parent 种群（适应度函数的值越小越好）
从 待选 parent 种群 中随机选择 2 个个体作为父方和母方。
抽取父母双方的染色体，进行交叉，产生 2 个子代。（交叉概率）
对子代（parent + 生成的 child）的染色体进行变异。（变异概率）
重复3,4,5步骤，直到新种群（parent_number + child_number）的产生。

循环以上步骤直至找到满意的解。

名词解释

交叉概率：两个个体进行交配的概率。例如，交配概率为0.8，则80%的“夫妻”会生育后代。
变异概率：所有的基因中发生变异的占总体的比例。

GA函数

function [best_fitness, elite, generation, last_generation] = my_ga( ...
    number_of_variables, ...    % 求解问题的参数个数
    fitness_function, ...       % 自定义适应度函数名
    population_size, ...        % 种群规模（每一代个体数目）
    parent_number, ...          % 每一代中保持不变的数目（除了变异）
    mutation_rate, ...          % 变异概率
    maximal_generation, ...     % 最大演化代数
    minimal_cost ...            % 最小目标值（函数值越小，则适应度越高）
)

% 累加概率
% 假设 parent_number = 10
% 分子 parent_number��1 用于生成一个数列
% 分母 sum(parent_number��1) 是一个求和结果（一个数）
%
% 分子 10     9     8     7     6     5     4     3     2     1
% 分母 55
% 相除 0.1818    0.1636    0.1455    0.1273    0.1091    0.0909    0.0727    0.0545    0.0364    0.0182
% 累加 0.1818    0.3455    0.4909    0.6182    0.7273    0.8182    0.8909    0.9455    0.9818    1.0000
%
% 运算结果可以看出
% 累加概率函数是一个从0到1增长得越来越慢的函数
% 因为后面加的概率越来越小（数列是降虚排列的）
cumulative_probabilities = cumsum((parent_number:-1:1) / sum(parent_number:-1:1)); % 1个长度为parent_number的数列

% 最佳适应度
% 每一代的最佳适应度都先初始化为1
best_fitness = ones(maximal_generation, 1);

% 精英
% 每一代的精英的参数值都先初始化为0
elite = zeros(maximal_generation, number_of_variables);

% 子女数量
% 种群数量 - 父母数量（父母即每一代中不发生改变的个体）
child_number = population_size - parent_number; % 每一代子女的数目

% 初始化种群
% population_size 对应矩阵的行，每一行表示1个个体，行数=个体数（种群数量）
% number_of_variables 对应矩阵的列，列数=参数个数（个体特征由这些参数表示）
population = rand(population_size, number_of_variables);

last_generation = 0; % 记录跳出循环时的代数


% 后面的代码都在for循环中
for generation = 1 : maximal_generation % 演化循环开始
    
    % feval把数据带入到一个定义好的函数句柄中计算
    % 把population矩阵带入fitness_function函数计算
    cost = feval(fitness_function, population); % 计算所有个体的适应度（population_size*1的矩阵）

    % index记录排序后每个值原来的行数
    [cost, index] = sort(cost); % 将适应度函数值从小到大排序

    % index(1:parent_number) 
    % 前parent_number个cost较小的个体在种群population中的行数
    % 选出这部分(parent_number个)个体作为父母，其实parent_number对应交叉概率
    population = population(index(1:parent_number), :); % 先保留一部分较优的个体
    % 可以看出population矩阵是不断变化的

    % cost在经过前面的sort排序后，矩阵已经改变为升序的
    % cost(1)即为本代的最佳适应度
    best_fitness(generation) = cost(1); % 记录本代的最佳适应度

    % population矩阵第一行为本代的精英个体
    elite(generation, :) = population(1, :); % 记录本代的最优解（精英）

    % 若本代的最优解已足够好，则停止演化
    if best_fitness(generation) < minimal_cost; 
        last_generation = generation;
        break; 
    end
    
    % 交叉变异产生新的种群

    % 染色体交叉开始
    for child = 1:2:child_number % 步长为2是因为每一次交叉会产生2个孩子
        
        % cumulative_probabilities长度为parent_number
        % 从中随机选择2个父母出来  (child+parent_number)%parent_number
        mother = find(cumulative_probabilities > rand, 1); % 选择一个较优秀的母亲
        father = find(cumulative_probabilities > rand, 1); % 选择一个较优秀的父亲
        
        % ceil（天花板）向上取整
        % rand 生成一个随机数
        % 即随机选择了一列，这一列的值交换
        crossover_point = ceil(rand*number_of_variables); % 随机地确定一个染色体交叉点
        
        % 假如crossover_point=3, number_of_variables=5
        % mask1 = 1     1     1     0     0
        % mask2 = 0     0     0     1     1
        mask1 = [ones(1, crossover_point), zeros(1, number_of_variables - crossover_point)];
        mask2 = not(mask1);
        
        % 获取分开的4段染色体
        % 注意是 .*
        mother_1 = mask1 .* population(mother, :); % 母亲染色体的前部分
        mother_2 = mask2 .* population(mother, :); % 母亲染色体的后部分
        
        father_1 = mask1 .* population(father, :); % 父亲染色体的前部分
        father_2 = mask2 .* population(father, :); % 父亲染色体的后部分
        
        % 得到下一代
        population(parent_number + child, :) = mother_1 + father_2; % 一个孩子
        population(parent_number+child+1, :) = mother_2 + father_1; % 另一个孩子
        
    end % 染色体交叉结束
    
    
    % 染色体变异开始
    
    % 变异种群
    mutation_population = population(2:population_size, :); % 精英不参与变异，所以从2开始
    
    number_of_elements = (population_size - 1) * number_of_variables; % 全部基因数目
    number_of_mutations = ceil(number_of_elements * mutation_rate); % 变异的基因数目（基因总数*变异率）
    
    % rand(1, number_of_mutations) 生成number_of_mutations个随机数(范围0-1)组成的矩阵(1*number_of_mutations)
    % 数乘后，矩阵每个元素表示发生改变的基因的位置（元素在矩阵中的一维坐标）
    mutation_points = ceil(number_of_elements * rand(1, number_of_mutations)); % 确定要变异的基因
    
    % 被选中的基因都被一个随机数替代，完成变异
    mutation_population(mutation_points) = rand(1, number_of_mutations); % 对选中的基因进行变异操作
    
    population(2:population_size, :) = mutation_population; % 发生变异之后的种群
    
    % 染色体变异结束
   
end % 演化循环结束

适应度函数

适应度函数由解决的问题决定。举一个平方和的例子。

求函数的最小值，其中每个变量的取值区间都是 [-1, +1]。问题的最优解：每个 x_i 都等于0。

function y = my_fitness(population)
% population是随机数[0,1]矩阵，下面的操作改变范围为[-1,1]
population = 2 * (population - 0.5); 
y = sum(population.^2, 2); % 行的平方和

测试

clear; 
close all;

% 调用 my_ga 进行计算
% 求解问题的参数个数         10
% 自定义适应度函数名         my_fitness
% 种群规模                  100
% 每一代中保持不变的数目     50 (即交叉率0.5)
% 变异概率                  0.1 (1/10的个体发生变异)
% 最大演化代数              10000 10000代
% 最小目标值                1.0e-6 个体适应度函数值 < 0.000001结束
[best_fitness, elite, generation, last_generation] = my_ga(10, 'my_fitness', 100, 50, 0.1, 10000, 1.0e-6);


% 输出后10行
% disp(best_fitness(9990:10000,:));
% disp(elite(9990:10000,:))
% 这样是不合适的，因为GA常常在中间就跳出循环了

% 这样才是合适的输出
disp(last_generation); 
i_begin = last_generation - 9;
disp(best_fitness(i_begin:last_generation,:));
% 将elite值转化为问题范围内
my_elite = elite(i_begin:last_generation,:);
my_elite = 2 * (my_elite - 0.5);
disp(my_elite);

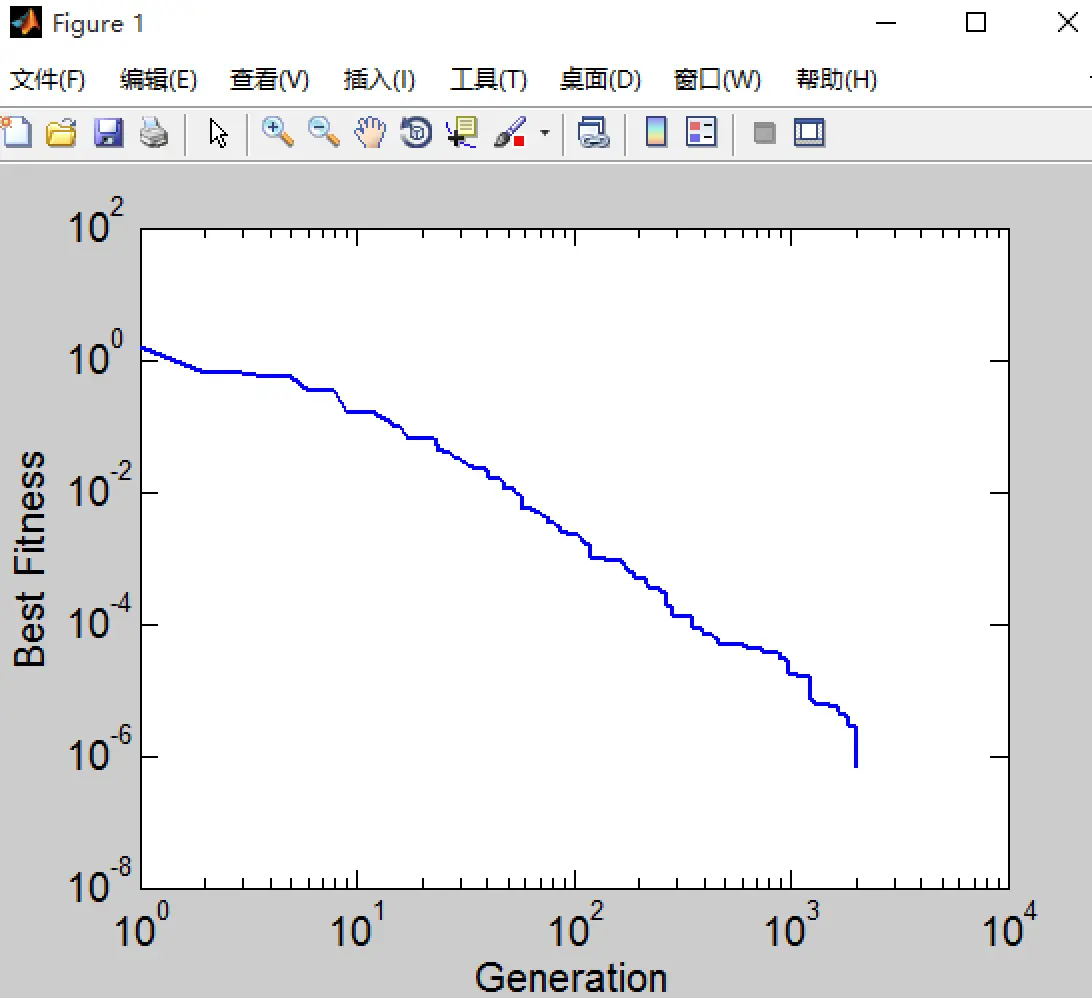
% 最佳适应度的演化情况
figure
loglog(1:generation, best_fitness(1:generation), 'linewidth',2)
xlabel('Generation','fontsize',15);
ylabel('Best Fitness','fontsize',15);
set(gca,'fontsize',15,'ticklength',get(gca,'ticklength')*2);

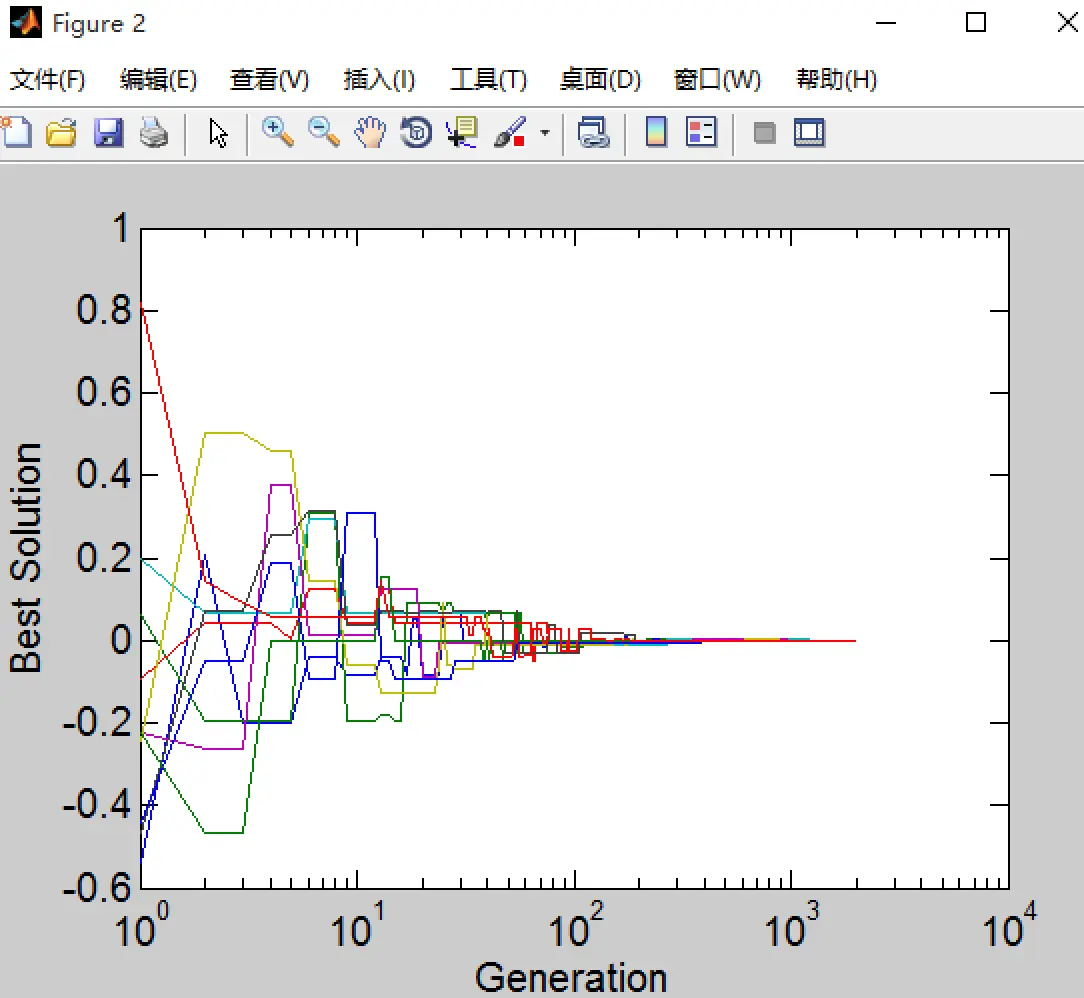
% 最优解的演化情况
figure
semilogx(1 : generation, 2 * elite(1 : generation, :) - 1)
xlabel('Generation','fontsize',15);
ylabel('Best Solution','fontsize',15);
set(gca,'fontsize',15,'ticklength',get(gca,'ticklength')*2);

输出

注意：这些值都是不确定的。

>> test_ga
        2035 // last_generation 跳出循环

   // best_fitness 后10行
   0.268244559363828
   0.268244559363828
   0.268244559363828
   0.268244559363828
   0.268244559363828
   0.268244559363828
   0.268244559363828
   0.268244559363828
   0.268244559363828
   0.063540829423325

  // elite 后10行，最后一行为想要的解
  Columns 1 through 7

  -0.000383439136218  -0.000401508032900   0.000097444596325   0.000337256996077  -0.000064973174152   0.000120384223563   0.000117039829849
  -0.000383439136218  -0.000401508032900   0.000097444596325   0.000337256996077  -0.000064973174152   0.000120384223563   0.000117039829849
  -0.000383439136218  -0.000401508032900   0.000097444596325   0.000337256996077  -0.000064973174152   0.000120384223563   0.000117039829849
  -0.000383439136218  -0.000401508032900   0.000097444596325   0.000337256996077  -0.000064973174152   0.000120384223563   0.000117039829849
  -0.000383439136218  -0.000401508032900   0.000097444596325   0.000337256996077  -0.000064973174152   0.000120384223563   0.000117039829849
  -0.000383439136218  -0.000401508032900   0.000097444596325   0.000337256996077  -0.000064973174152   0.000120384223563   0.000117039829849
  -0.000383439136218  -0.000401508032900   0.000097444596325   0.000337256996077  -0.000064973174152   0.000120384223563   0.000117039829849
  -0.000383439136218  -0.000401508032900   0.000097444596325   0.000337256996077  -0.000064973174152   0.000120384223563   0.000117039829849
  -0.000383439136218  -0.000401508032900   0.000097444596325   0.000337256996077  -0.000064973174152   0.000120384223563   0.000117039829849
  -0.000383439136218  -0.000401508032900   0.000097444596325   0.000337256996077  -0.000064973174152   0.000120384223563   0.000117039829849

  Columns 8 through 10

  -0.000362645135942  -0.001433818552852   0.000176675571817
  -0.000362645135942  -0.001433818552852   0.000176675571817
  -0.000362645135942  -0.001433818552852   0.000176675571817
  -0.000362645135942  -0.001433818552852   0.000176675571817
  -0.000362645135942  -0.001433818552852   0.000176675571817
  -0.000362645135942  -0.001433818552852   0.000176675571817
  -0.000362645135942  -0.001433818552852   0.000176675571817
  -0.000362645135942  -0.001433818552852   0.000176675571817
  -0.000362645135942  -0.001433818552852   0.000176675571817
  -0.000362645135942  -0.000093799483467   0.000176675571817

趋势图

最佳适应度函数的值

elite 的变化趋势，10条折线 -> 10个变量

文章参考

科学网 - 一个用matlab实现的50行的遗传算法程序

genetic-algorithm

遗传算法 - 简书

GA函数

适应度函数

测试

输出

趋势图

文章参考

同类工具

相关阅读

相关文章

相关问答

相关文档