java数据结构之树基本概念解析及代码示例

Java中树的存储结构实现 一、树 树与线性表、栈、队列等线性结构不同,树是一...节点与节点之间的父子关系,可以为每个节点增加一个parent域,用以记录该节点的父点

树是一种抽象数据类型（ADT）或是实作这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由n（n>0）个有限节点组成一个具有层次关系的集合。把 它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

树定义和基本术语

定义

树(Tree)是n(n≥0)个结点的有限集T，并且当n＞0时满足下列条件：

（1）有且仅有一个特定的称为根(Root)的结点；

（2）当n＞1时，其余结点可以划分为m(m＞0)个互不相交的有限集T1、T2、…、Tm，每个集Ti(1≤i≤m)均为树，且称为树T的子树(SubTree)。

特别地，不含任何结点(即n＝0)的树，称为空树。

如下就是一棵树的结构：

基本术语

结点：存储数据元素和指向子树的链接，由数据元素和构造数据元素之间关系的引用组成。
孩子结点：树中一个结点的子树的根结点称为这个结点的孩子结点，如图1中的A的孩子结点有B、C、D
双亲结点：树中某个结点有孩子结点(即该结点的度不为0)，该结点称为它孩子结点的双亲结点，也叫前驱结点。双亲结点和孩子结点是相互的，如图1中，A的孩子结点是B、C、D，B、C、D的双亲结点是A。
兄弟结点：具有相同双亲结点(即同一个前驱)的结点称为兄弟结点，如图1中B、B、D为兄弟结点。
结点的度：结点所有子树的个数称为该结点的度，如图1，A的度为3，B的度为2.
树的度：树中所有结点的度的最大值称为树的度，如图1的度为3.
叶子结点：度为0的结点称为叶子结点，也叫终端结点。如图1的K、L、F、G、M、I、J
分支结点：度不为0的结点称为分支结点，也叫非终端结点。如图1的A、B、C、D、E、H
结点的层次：从根结点到树中某结点所经路径的分支数称为该结点的层次。根结点的层次一般为1(也可以自己定义为0)，这样，其它结点的层次是其双亲结点的层次加1.
树的深度：树中所有结点的层次的最大值称为该树的深度(也就是最下面那个结点的层次)。
有序树和无序树：树中任意一个结点的各子树按从左到右是有序的，称为有序树，否则称为无序树。
树的抽象数据类型描述
数据元素：具有相同特性的数据元素的集合。
结构关系：树中数据元素间的结构关系由树的定义确定。

基本操作：树的主要操作有

（1）创建树IntTree(&T)
         创建1个空树T。
（2）销毁树DestroyTree(&T)
（3）构造树CreatTree(&T，deinition)
（4）置空树ClearTree(&T)
          将树T置为空树。
（5）判空树TreeEmpty(T)
（6）求树的深度TreeDepth(T)
（7）获得树根Root(T)
（8）获取结点Value(T，cur_e，&e)
         将树中结点cur_e存入e单元中。
（9）数据赋值Assign(T，cur_e，value)
         将结点value，赋值于树T的结点cur_e中。
（10）获得双亲Parent(T，cur_e)
        返回树T中结点cur_e的双亲结点。
（11）获得最左孩子LeftChild(T，cur_e)
        返回树T中结点cur_e的最左孩子。
（12）获得右兄弟RightSibling(T，cur_e)
        返回树T中结点cur_e的右兄弟。
（13）插入子树InsertChild(&T，&p，i，c)
      将树c插入到树T中p指向结点的第i个子树之前。
（14）删除子树DeleteChild(&T，&p，i)
       删除树T中p指向结点的第i个子树。
（15）遍历树TraverseTree(T，visit())

树的实现

树是一种递归结构，表示方式一般有孩子表示法和孩子兄弟表示法两种。树实现方式有很多种、有可以由广义表的递归实现，也可以有二叉树实现，其中最常见的是将树用孩子兄弟表示法转化成二叉树来实现。

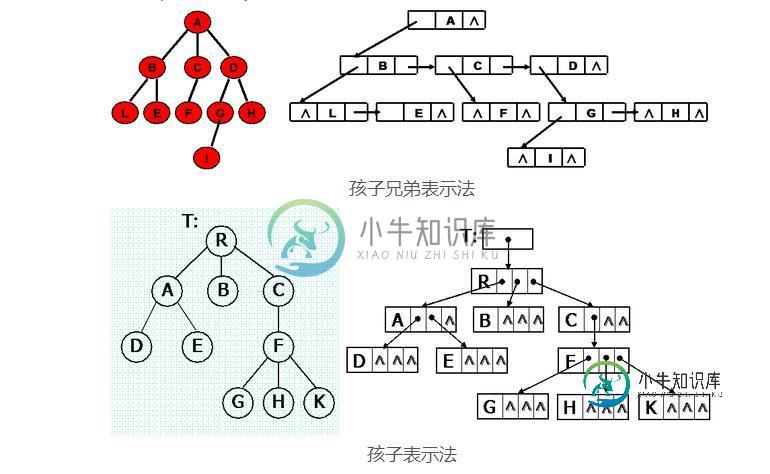
下面以孩子表示法为例讲一下树的实现：

树的定义和实现

package datastructure.tree;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;
/** 
   * 树的定义和实现 
   * @author Administrator 
   * 
   */
public class Tree {
	private Object data;
	private List<Tree> childs;
	public Tree(){
		data = null;
		childs = new ArrayList();
		childs.clear();
	}
	public Tree(Object data) {
		this.data = data;
		childs = new ArrayList();
		childs.clear();
	}
	/** 
     * 添加子树 
     * @param tree 子树 
     */
	public void addNode(Tree tree) {
		childs.add(tree);
	}
	/** 
     * 置空树 
     */
	public void clearTree() {
		data = null;
		childs.clear();
	}
	/** 
     * 求树的深度 
     * 这方法还有点问题，有待完善 
     * @return 树的深度 
     */
	public int dept() {
		return dept(this);
	}
	/** 
     * 求树的深度 
     * 这方法还有点问题，有待完善 
     * @param tree 
     * @return 
     */
	private int dept(Tree tree) {
		if(tree.isEmpty()) {
			return 0;
		} else if(tree.isLeaf()) {
			return 1;
		} else {
			int n = childs.size();
			int[] a = new int[n];
			for (int i=0; i<n; i++) {
				if(childs.get(i).isEmpty()) {
					a[i] = 0+1;
				} else {
					a[i] = dept(childs.get(i)) + 1;
				}
			}
			Arrays.sort(a);
			return a[n-1];
		}
	}
	/** 
     * 返回递i个子树 
     * @param i 
     * @return 
     */
	public Tree getChild(int i) {
		return childs.get(i);
	}
	/** 
     * 求第一个孩子 结点 
     * @return 
     */
	public Tree getFirstChild() {
		return childs.get(0);
	}
	/** 
     * 求最后 一个孩子结点 
     * @return 
     */
	public Tree getLastChild() {
		return childs.get(childs.size()-1);
	}
	public List<Tree> getChilds() {
		return childs;
	}
	/** 
     * 获得根结点的数据 
     * @return 
     */
	public Object getRootData() {
		return data;
	}
	/** 
     * 判断是否为空树 
     * @return 如果为空，返回true,否则返回false 
     */
	public Boolean isEmpty() {
		if(childs.isEmpty() && data == null) 
		        return true;
		return false;
	}
	/** 
     * 判断是否为叶子结点 
     * @return 
     */
	public Boolean isLeaf() {
		if(childs.isEmpty()) 
		        return true;
		return false;
	}
	/** 
     * 获得树根 
     * @return 树的根 
     */
	public Tree root() {
		return this;
	}
	/** 
     * 设置根结点的数据 
     */
	public void setRootData(Object data) {
		this.data = data;
	}
	/** 
     * 求结点数 
     * 这方法还有点问题，有待完善 
     * @return 结点的个数 
     */
	public int size() {
		return size(this);
	}
	/** 
     * 求结点数 
     * 这方法还有点问题，有待完善 
     * @param tree 
     * @return 
     */
	private int size(Tree tree) {
		if(tree.isEmpty()) {
			return 0;
		} else if(tree.isLeaf()) {
			return 1;
		} else {
			int count = 1;
			int n = childs.size();
			for (int i=0; i<n; i++) {
				if(!childs.get(i).isEmpty()) {
					count += size(childs.get(i));
				}
			}
			return count;
		}
	}
}

树的遍历

树的遍历有两种

前根遍历

（1）.访问根结点；

（2）.按照从左到右的次序行根遍历根结点的第一棵子树；

后根遍历

（1）.按照从左到右的次序行根遍历根结点的第一棵子树；

（2）.访问根结点；

Visit.Java

package datastructure.tree;
import datastructure.tree.btree.BTree;
/** 
   * 对结点进行操作的接口,规定树的遍历的类必须实现这个接口 
   * @author Administrator 
   * 
   */
public interface Visit {
	/** 
     * 对结点进行某种操作 
     * @param btree 树的结点 
     */
	public void visit(BTree btree);
}

order.java

package datastructure.tree;
import java.util.List;
/** 
   * 树的遍历 
   * @author Administrator 
   * 
   */
public class Order {
	/** 
     * 先根遍历 
     * @param root 要的根结点 
     */
	public void preOrder(Tree root) {
		if(!root.isEmpty()) {
			visit(root);
			for (Tree child : root.getChilds()) {
				if(child != null) {
					preOrder(child);
				}
			}
		}
	}
	/** 
     * 后根遍历 
     * @param root 树的根结点 
     */
	public void postOrder(Tree root) {
		if(!root.isEmpty()) {
			for (Tree child : root.getChilds()) {
				if(child != null) {
					preOrder(child);
				}
			}
			visit(root);
		}
	}
	public void visit(Tree tree) {
		System.out.print("\t" + tree.getRootData());
	}
}

测试：

要遍历的树如下：

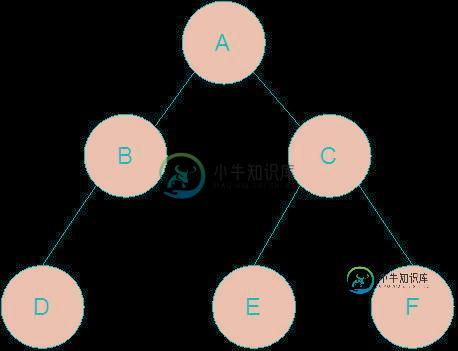
package datastructure.tree;
import java.util.Iterator;
import java.util.Scanner;
public class TreeTest {
	/** 
     * @param args 
     */
	public static void main(String[] args) {
		Tree root = new Tree("A");
		root.addNode(new Tree("B"));
		root.addNode(new Tree("C"));
		root.addNode(new Tree("D"));
		Tree t = null;
		t = root.getChild(0);
		t.addNode(new Tree("L"));
		t.addNode(new Tree("E"));
		t = root.getChild(1);
		t.addNode(new Tree("F"));
		t = root.getChild(2);
		t.addNode(new Tree("I"));
		t.addNode(new Tree("H"));
		t = t.getFirstChild();
		t.addNode(new Tree("L"));
		System.out.println("first node:" + root.getRootData());
		//System.out.println("size:" + root.size()); 
		//System.out.println("dept:" + root.dept()); 
		System.out.println("is left:" + root.isLeaf());
		System.out.println("data:" + root.getRootData());
		Order order = new Order();
		System.out.println("前根遍历：");
		order.preOrder(root);
		System.out.println("\n后根遍历：");
		order.postOrder(root);
	}
}

结果：

first node:A
is left:false
data:A
前根遍历：
A BL E C F DI L H
后根遍历：
B LE C F D IL H A

结束语：

以上就是本文关于java数据结构之树基本概念解析及代码示例的全部内容，希望对大家有所帮助。感兴趣的朋友可以继续参阅本站：

Java编程求二叉树的镜像两种方法介绍

java算法实现红黑树完整代码示例

java实现遍历树形菜单两种实现代码分享

如有不足之处，欢迎留言指出。