C++ 中二分查找递归非递归实现并分析
C++ 中二分查找递归非递归实现并分析
二分查找在有序数列的查找过程中算法复杂度低,并且效率很高。因此较为受我们追捧。其实二分查找算法,是一个很经典的算法。但是呢,又容易写错。因为总是考虑不全边界问题。
用非递归简单分析一下,在编写过程中,如果编写的是以下的代码:
#include<iostream> #include<assert.h> using namespace std; int binaty_search(int* arr, size_t n, int x) { assert(arr); int left = 0; int right = n - 1; while (left <= right) { int mid = (left + right) / 2; if (x < arr[mid]) { right = mid-1; } else if (x > arr[mid]) { left = mid+1; } else return mid; } return -1; } int main() { int arr[] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }; cout << binaty_search(arr, sizeof(arr) / sizeof(int), 0) << endl; cout << binaty_search(arr, sizeof(arr) / sizeof(int), 1) << endl; cout << binaty_search(arr, sizeof(arr) / sizeof(int), 2) << endl; cout << binaty_search(arr, sizeof(arr) / sizeof(int), 3) << endl; cout << binaty_search(arr, sizeof(arr) / sizeof(int), 4) << endl; cout << binaty_search(arr, sizeof(arr) / sizeof(int), 5) << endl; cout << binaty_search(arr, sizeof(arr) / sizeof(int), 6) << endl; cout << binaty_search(arr, sizeof(arr) / sizeof(int), 7) << endl; cout << binaty_search(arr, sizeof(arr) / sizeof(int), 8) << endl; cout << binaty_search(arr, sizeof(arr) / sizeof(int), 9) << endl; cout << binaty_search(arr, sizeof(arr) / sizeof(int), 10) << endl; return 0; }
那么我们可以简单分析一下:
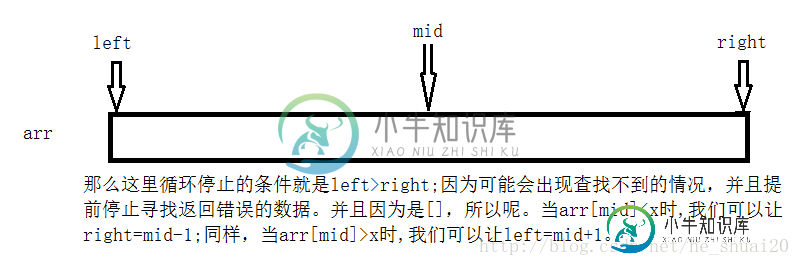
如果是以下这样的代码实现:
#include<iostream>
#include<assert.h>
using namespace std;
int binaty_search(int* arr, size_t n, int x)
{
assert(arr);
int left = 0;
int right = n;
while (left < right)
{
int mid = (left + right) / 2;
if (x < arr[mid])
{
right = mid;
}
else if (x > arr[mid])
{
left = mid + 1;
}
else
return mid;
}
return -1;
}
int main()
{
int arr[] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 };
cout << binaty_search(arr, sizeof(arr) / sizeof(int), 0) << endl;
cout << binaty_search(arr, sizeof(arr) / sizeof(int), 1) << endl;
cout << binaty_search(arr, sizeof(arr) / sizeof(int), 2) << endl;
cout << binaty_search(arr, sizeof(arr) / sizeof(int), 3) << endl;
cout << binaty_search(arr, sizeof(arr) / sizeof(int), 4) << endl;
cout << binaty_search(arr, sizeof(arr) / sizeof(int), 5) << endl;
cout << binaty_search(arr, sizeof(arr) / sizeof(int), 6) << endl;
cout << binaty_search(arr, sizeof(arr) / sizeof(int), 7) << endl;
cout << binaty_search(arr, sizeof(arr) / sizeof(int), 8) << endl;
cout << binaty_search(arr, sizeof(arr) / sizeof(int), 9) << endl;
cout << binaty_search(arr, sizeof(arr) / sizeof(int), 10) << endl;
return 0;
}
那么可以简单分析一下为:

同样,递归实现的条件也分为两种,我就只演示一种,代码如下:
#include<iostream>
#include<assert.h>
using namespace std;
int binaty_srarch(int* arr, int x, int left, int right)
{
assert(arr);
int mid;
if (left <= right)
{
mid = (left + right) / 2;
if (arr[mid] == x)
{
return mid;
}
else
if (x < arr[mid])
{
return binaty_srarch(arr, x, left, right - 1);
}
else if (x>arr[mid])
{
return binaty_srarch(arr, x, left + 1, right);
}
}
return -1;
}
int main()
{
int arr[] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 };
cout << binaty_srarch(arr, 0, 0, (sizeof(arr) / sizeof(int)) - 1) << endl;
cout << binaty_srarch(arr, 1, 0, (sizeof(arr) / sizeof(int)) - 1) << endl;
cout << binaty_srarch(arr, 2, 0, (sizeof(arr) / sizeof(int)) - 1) << endl;
cout << binaty_srarch(arr, 3, 0, (sizeof(arr) / sizeof(int)) - 1) << endl;
cout << binaty_srarch(arr, 4, 0, (sizeof(arr) / sizeof(int)) - 1) << endl;
cout << binaty_srarch(arr, 5, 0, (sizeof(arr) / sizeof(int)) - 1) << endl;
cout << binaty_srarch(arr, 6, 0, (sizeof(arr) / sizeof(int)) - 1) << endl;
cout << binaty_srarch(arr, 7, 0, (sizeof(arr) / sizeof(int)) - 1) << endl;
cout << binaty_srarch(arr, 8, 0, (sizeof(arr) / sizeof(int)) - 1) << endl;
cout << binaty_srarch(arr, 9, 0, (sizeof(arr) / sizeof(int)) - 1) << endl;
cout << binaty_srarch(arr, 10, 0, (sizeof(arr) / sizeof(int)) - 1) << endl;
return 0;
}
感谢阅读,希望能帮助到大家,谢谢大家对本站的支持!
-
本文向大家介绍用非递归方法实现二分查找相关面试题,主要包含被问及用非递归方法实现二分查找时的应答技巧和注意事项,需要的朋友参考一下 --代码如下,二分查找只适用于有序数列,对其进行查找,效率非常高,不适用于无序数列
-
我正在处理一个递归二分法/算法。我已经把我的递归放在else/else if语句中,不知道我是否错了。它也返回正确的根,而没有递归,但主要问题是用递归。
-
我有TreeNode类——非二叉树(
-
null 请记住,我是一个非常早期,初学者,婴儿程序员和DIY课,我正在学习的糟糕的解释东西。所以请简单明了。谢谢你。
-
主要内容:递归实现,非递归实现二叉树中序遍历的实现思想是: 访问当前节点的左子树; 访问根节点; 访问当前节点的右子树; 图 1 二叉树 以图 1 为例,采用中序遍历的思想遍历该二叉树的过程为: 访问该二叉树的根节点,找到 1; 遍历节点 1 的左子树,找到节点 2; 遍历节点 2 的左子树,找到节点 4; 由于节点 4 无左孩子,因此找到节点 4,并遍历节点 4 的右子树; 由于节点 4 无右子树,因此节点 2 的左子
-
主要内容:递归实现,非递归实现二叉树后序遍历的实现思想是:从根节点出发,依次遍历各节点的左右子树,直到当前节点左右子树遍历完成后,才访问该节点元素。 图 1 二叉树 如图 1 中,对此二叉树进行后序遍历的操作过程为: 从根节点 1 开始,遍历该节点的左子树(以节点 2 为根节点); 遍历节点 2 的左子树(以节点 4 为根节点); 由于节点 4 既没有左子树,也没有右子树,此时访问该节点中的元素 4,并回退到节点 2 ,遍

