java算法实现红黑树完整代码示例

红黑树

定义

红黑树（英语：Red–black tree）是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。

红黑树的另一种定义是含有红黑链接并满足下列条件的二叉查找树：

红链接均为左链接；没有任何一个结点同时和两条红链接相连；该树是完美黑色平衡的，即任意空链接到根结点的路径上的黑链接数量相同。

满足这样定义的红黑树和相应的2-3树是一一对应的。

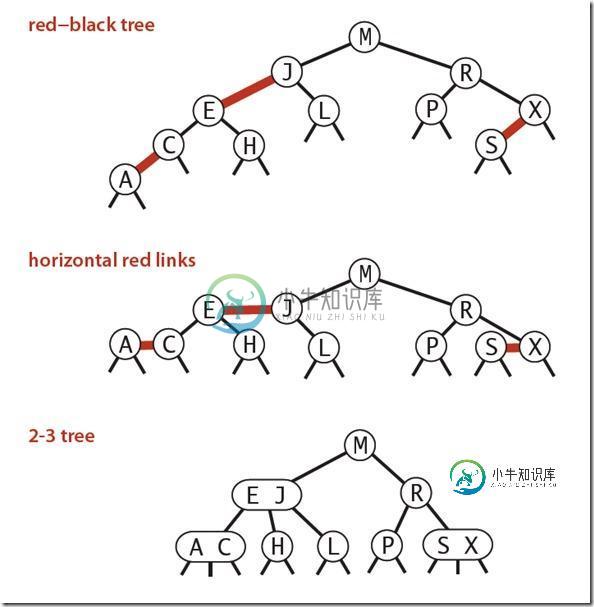
旋转

旋转又分为左旋和右旋。通常左旋操作用于将一个向右倾斜的红色链接旋转为向左链接。对比操作前后，可以看出，该操作实际上是将红线链接的两个节点中的一个较大的节点移动到根节点上。

左旋操作如下图：

右旋旋操作如下图：

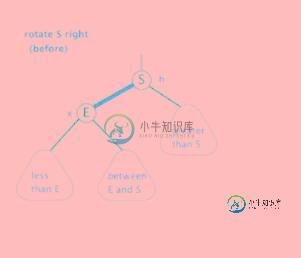
即：

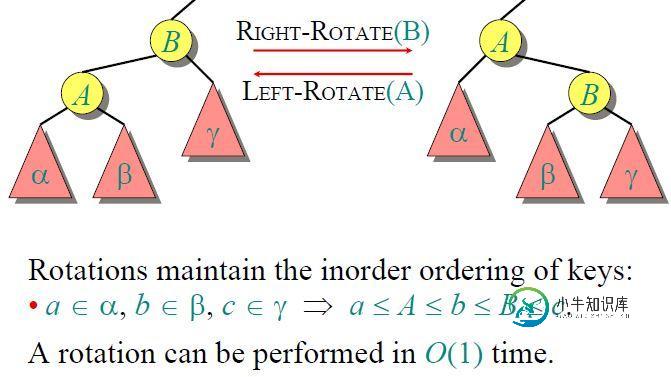
复杂度

红黑树的平均高度大约为lgN。

下图是红黑树在各种情况下的时间复杂度，可以看出红黑树是2-3查找树的一种实现，他能保证最坏情况下仍然具有对数的时间复杂度。

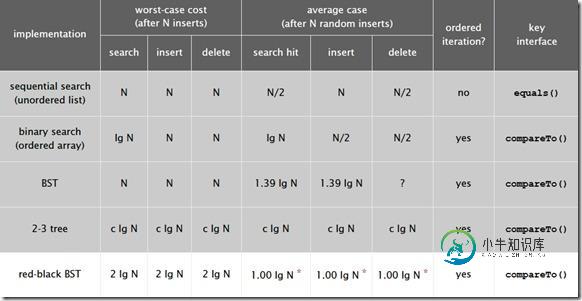
Java代码

import java.util.NoSuchElementException;
import java.util.Scanner;
public class RedBlackBST<key extends="" key="">, Value> {
  private static final boolean RED = true;
  private static final boolean BLACK = false;
  private Node root; //root of the BST
  private class Node {
    private Key key;      //key
    private Value val;     //associated data
    private Node left, right;  //links to left and right subtrees
    private boolean color;   //color of parent link
    private int size;      //subtree count
    public Node(Key key, Value val, boolean color, int size) {
      this.key = key;
      this.val = val;
      this.color = color;
      this.size = size;
    }
  }
  //is node x red?
  private boolean isRed(Node x) {
    if(x == null) {
      return false;
    }
    return x.color == RED;
  }
  //number of node in subtree rooted at x; 0 if x is null
  private int size(Node x) {
    if(x == null) {
      return 0;
    }
    return x.size;
  }  
  /**
   * return the number of key-value pairs in this symbol table
   * @return the number of key-value pairs in this symbol table
   */
  public int size() {
    return size(root);
  }
  /**
   * is this symbol table empty?
   * @return true if this symbol table is empty and false otherwise
   */
  public boolean isEmpty() {
    return root == null;
  }
  /**
   * return the value associated with the given key
   * @param key the key
   * @return the value associated with the given key if the key is in the symbol table, and null if it is not.
   */
  public Value get(Key key) {
    if(key == null) {
      throw new NullPointerException("argument to get() is null");
    }
    return get(root, key);
  }
  //value associated with the given key in subtree rooted at x; null if no such key
  private Value get(Node x, Key key) {
    while(x != null) {
      int cmp = key.compareTo(x.key);
      if(cmp < 0) {
        x = x.left;
      }
      else if(cmp > 0) {
        x = x.right;
      }
      else {
        return x.val;
      }        
    }
    return null;
  }
  /**
   * does this symbol table contain the given key?
   * @param key the key
   * @return true if this symbol table contains key and false otherwise
   */
  public boolean contains(Key key) {
    return get(key) != null;
  }
  /***************************************************************************
  * Red-black tree insertion.
  ***************************************************************************/
  /**
   * Inserts the specified key-value pair into the symbol table, overwriting the old 
   * value with the new value if the symbol table already contains the specified key.
   * Deletes the specified key (and its associated value) from this symbol table
   * if the specified value is null.
   *
   * @param key the key
   * @param val the value
   * @throws NullPointerException if key is null
   */
  public void put(Key key, Value val) {
    if (key == null) {
      throw new NullPointerException("first argument to put() is null");
    }
    if (val == null) {
      delete(key);
      return;
    }
    root = put(root, key, val);
    root.color = BLACK;    
  }
  // insert the key-value pair in the subtree rooted at h
  private Node put(Node h, Key key, Value val) {
    if(h == null) {
      return new Node(key, val, RED, 1);
    }
    int cmp = key.compareTo(h.key);
    if(cmp < 0) {
      h.left = put(h.left, key, val);
    }
    else if(cmp > 0) {
      h.right = put(h.right, key, val);
    }
    else {
      h.val = val;
    }
    if(isRed(h.right) && !isRed(h.left)) {
      h = rotateLeft(h);
    }
    if(isRed(h.left) && isRed(h.left.left)) {
      h = rotateRight(h);
    }
    if(isRed(h.left) && isRed(h.right)) {
      flipColors(h);
    }
    h.size = size(h.left) + size(h.right) + 1;
    return h;
  }
  /***************************************************************************
  * Red-black tree deletion.
  ***************************************************************************/
 
  /**
   * Removes the smallest key and associated value from the symbol table.
   * @throws NoSuchElementException if the symbol table is empty
   */
  public void deleteMin() {
    if (isEmpty()) {
      throw new NoSuchElementException("BST underflow");
    }
    // if both children of root are black, set root to red
    if (!isRed(root.left) && !isRed(root.right))
      root.color = RED;
    root = deleteMin(root);
    if (!isEmpty()) root.color = BLACK;
    // assert check();
  }
  // delete the key-value pair with the minimum key rooted at h
  // delete the key-value pair with the minimum key rooted at h
  private Node deleteMin(Node h) { 
    if (h.left == null){
      return null;
    }
    if (!isRed(h.left) && !isRed(h.left.left)) {
      h = moveRedLeft(h);
    }
    h.left = deleteMin(h.left);
    return balance(h);
  }
  /**
   * Removes the largest key and associated value from the symbol table.
   * @throws NoSuchElementException if the symbol table is empty
   */
  public void deleteMax() {
    if (isEmpty()) {
      throw new NoSuchElementException("BST underflow");
    }
    // if both children of root are black, set root to red
    if (!isRed(root.left) && !isRed(root.right))
      root.color = RED;
    root = deleteMax(root);
    if (!isEmpty()) root.color = BLACK;
    // assert check();
  }
  // delete the key-value pair with the maximum key rooted at h
  // delete the key-value pair with the maximum key rooted at h
  private Node deleteMax(Node h) { 
      if (isRed(h.left))
        h = rotateRight(h);
      if (h.right == null)
        return null;
      if (!isRed(h.right) && !isRed(h.right.left))
        h = moveRedRight(h);
      h.right = deleteMax(h.right);
      return balance(h);
    }
  /**
   * remove the specified key and its associated value from this symbol table   
   * (if the key is in this symbol table).  
   *
   * @param key the key
   * @throws NullPointerException if key is null
   */
  public void delete(Key key) {
    if (key == null) {
      throw new NullPointerException("argument to delete() is null");
    }
    if (!contains(key)) {
      return;
    }
    //if both children of root are black, set root to red
    if(!isRed(root.left) && !isRed(root.right)) {
      root.color = RED;
    }
    root = delete(root, key);
    if(!isEmpty()) {
      root.color = BLACK;
    }
  }
  // delete the key-value pair with the given key rooted at h
  // delete the key-value pair with the given key rooted at h
  private Node delete(Node h, Key key) {
    if(key.compareTo(h.key) < 0) {
      if(!isRed(h.left) && !isRed(h.left.left)) {
        h = moveRedLeft(h);
      }
      h.left = delete(h.left, key);
    }
    else {
      if(isRed(h.left)) {
        h = rotateRight(h);
      }
      if (key.compareTo(h.key) == 0 && (h.right == null)) {
        return null;
      }
      if (!isRed(h.right) && !isRed(h.right.left)) {
        h = moveRedRight(h);
      }
      if (key.compareTo(h.key) == 0) {
        Node x = min(h.right);
        h.key = x.key;
        h.val = x.val;
        h.right = deleteMin(h.right);
      }
      else {
        h.right = delete(h.right, key);
      }
    }
    return balance(h);
  }
  /***************************************************************************
  * Red-black tree helper functions.
  ***************************************************************************/
  // make a left-leaning link lean to the right
  // make a left-leaning link lean to the right
  private Node rotateRight(Node h) {
    // assert (h != null) && isRed(h.left);
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    x.color = x.right.color;
    x.right.color = RED;
    x.size = h.size;
    h.size = size(h.left) + size(h.right) + 1;
    return x;
  }
  // make a right-leaning link lean to the left
  // make a right-leaning link lean to the left
  private Node rotateLeft(Node h) {
    // assert (h != null) && isRed(h.right);
    Node x = h.right;
    h.right = x.left;
    x.left = h;
    x.color = x.left.color;
    x.left.color = RED;
    x.size = h.size;
    h.size = size(h.left) + size(h.right) + 1;
    return x;
  }
  // flip the colors of a node and its two children
  // flip the colors of a node and its two children
  private void flipColors(Node h) {
    // h must have opposite color of its two children
    // assert (h != null) && (h.left != null) && (h.right != null);
    // assert (!isRed(h) && isRed(h.left) && isRed(h.right))
    //  || (isRed(h) && !isRed(h.left) && !isRed(h.right));
    h.color = !h.color;
    h.left.color = !h.left.color;
    h.right.color = !h.right.color;
  }
  // Assuming that h is red and both h.left and h.left.left
  // are black, make h.left or one of its children red.
  // Assuming that h is red and both h.left and h.left.left
  // are black, make h.left or one of its children red.
  private Node moveRedLeft(Node h) {
    // assert (h != null);
    // assert isRed(h) && !isRed(h.left) && !isRed(h.left.left);
    flipColors(h);
    if (isRed(h.right.left)) { 
      h.right = rotateRight(h.right);
      h = rotateLeft(h);
      flipColors(h);
    }
    return h;
  }
  // Assuming that h is red and both h.right and h.right.left
  // are black, make h.right or one of its children red.
  // Assuming that h is red and both h.right and h.right.left
  // are black, make h.right or one of its children red.
  private Node moveRedRight(Node h) {
    // assert (h != null);
    // assert isRed(h) && !isRed(h.right) && !isRed(h.right.left);
    flipColors(h);
    if (isRed(h.left.left)) { 
      h = rotateRight(h);
      flipColors(h);
    }
    return h;
  }
  // restore red-black tree invariant
  // restore red-black tree invariant
  private Node balance(Node h) {
    // assert (h != null);
    if (isRed(h.right)) {
      h = rotateLeft(h);
    }
    if (isRed(h.left) && isRed(h.left.left)) {
      h = rotateRight(h);
    }
    if (isRed(h.left) && isRed(h.right)) {
      flipColors(h);
    }
    h.size = size(h.left) + size(h.right) + 1;
    return h;
  }
  /***************************************************************************
   * Utility functions.
   ***************************************************************************/
   /**
   * Returns the height of the BST (for debugging).
   * @return the height of the BST (a 1-node tree has height 0)
   */
   public int height() {
     return height(root);
   }
   private int height(Node x) {
     if (x == null) {
       return -1;
     }
     return 1 + Math.max(height(x.left), height(x.right));
   }
  /***************************************************************************
   * Ordered symbol table methods.
   ***************************************************************************/
   /**
   * Returns the smallest key in the symbol table.
   * @return the smallest key in the symbol table
   * @throws NoSuchElementException if the symbol table is empty
   */
   public Key min() {
     if (isEmpty()) {
       throw new NoSuchElementException("called min() with empty symbol table");
     }
     return min(root).key;
   } 
   // the smallest key in subtree rooted at x; null if no such key
   private Node min(Node x) { 
     // assert x != null;
     if (x.left == null) {
       return x; 
     }
     else {
       return min(x.left); 
     }
   } 
   /**
   * Returns the largest key in the symbol table.
   * @return the largest key in the symbol table
   * @throws NoSuchElementException if the symbol table is empty
   */
   public Key max() {
     if (isEmpty()) {
       throw new NoSuchElementException("called max() with empty symbol table");
     }
     return max(root).key;
   } 
   // the largest key in the subtree rooted at x; null if no such key
   private Node max(Node x) { 
     // assert x != null;
     if (x.right == null) {
       return x; 
     }
     else {
       return max(x.right);     
     }
   } 
   /**
   * Returns the largest key in the symbol table less than or equal to key.
   * @param key the key
   * @return the largest key in the symbol table less than or equal to key
   * @throws NoSuchElementException if there is no such key
   * @throws NullPointerException if key is null
   */
   public Key floor(Key key) {
     if (key == null) {
       throw new NullPointerException("argument to floor() is null");
     }
     if (isEmpty()) {
       throw new NoSuchElementException("called floor() with empty symbol table");
     }
     Node x = floor(root, key);
     if (x == null) {
       return null;     
     }
     else {
       return x.key;
     }
   }  
   // the largest key in the subtree rooted at x less than or equal to the given key
   private Node floor(Node x, Key key) {
     if (x == null) {
       return null;
     }
     int cmp = key.compareTo(x.key);
     if (cmp == 0) {
       return x;
     }
     if (cmp < 0) {
       return floor(x.left, key);     
     }
     Node t = floor(x.right, key);
     if (t != null) {
       return t;     
     }
     else {
       return x;
     }
   }
   /**
   * Returns the smallest key in the symbol table greater than or equal to key.
   * @param key the key
   * @return the smallest key in the symbol table greater than or equal to key
   * @throws NoSuchElementException if there is no such key
   * @throws NullPointerException if key is null
   */
   public Key ceiling(Key key) {
     if (key == null) {
       throw new NullPointerException("argument to ceiling() is null");
     }
     if (isEmpty()) {
       throw new NoSuchElementException("called ceiling() with empty symbol table");
     }
     Node x = ceiling(root, key);
     if (x == null) {
       return null;
     }
     else {
       return x.key; 
     }
   }
   // the smallest key in the subtree rooted at x greater than or equal to the given key
   private Node ceiling(Node x, Key key) { 
     if (x == null) {
       return null;
     }     
     int cmp = key.compareTo(x.key);
     if (cmp == 0) {
       return x;
     }
     if (cmp > 0) {
       return ceiling(x.right, key);
     }
     Node t = ceiling(x.left, key);
     if (t != null) {
       return t; 
     }
     else {
       return x;
     }
   }
   /**
   * Return the kth smallest key in the symbol table.
   * @param k the order statistic
   * @return the kth smallest key in the symbol table
   * @throws IllegalArgumentException unless k is between 0 and
   *   <em>N</em> − 1
   */
   public Key select(int k) {
     if (k < 0 || k >= size()) {
       throw new IllegalArgumentException();
     }
     Node x = select(root, k);
     return x.key;
   }
   // the key of rank k in the subtree rooted at x
   private Node select(Node x, int k) {
     // assert x != null;
     // assert k >= 0 && k < size(x);
     int t = size(x.left); 
     if   (t > k) {
       return select(x.left, k); 
     }
     else if (t < k) {
       return select(x.right, k-t-1); 
     }
     else {
       return x; 
     }
   } 
   /**
   * Return the number of keys in the symbol table strictly less than key.
   * @param key the key
   * @return the number of keys in the symbol table strictly less than key
   * @throws NullPointerException if key is null
   */
   public int rank(Key key) {
     if (key == null) {
       throw new NullPointerException("argument to rank() is null");
     }
     return rank(key, root);
   } 
   // number of keys less than key in the subtree rooted at x
   private int rank(Key key, Node x) {
     if (x == null) {
       return 0; 
     }
     int cmp = key.compareTo(x.key); 
     if   (cmp < 0) {
       return rank(key, x.left); 
     }
     else if (cmp > 0) {
       return 1 + size(x.left) + rank(key, x.right); 
     }
     else {
       return size(x.left); 
     }
   } 
  /***************************************************************************
   * Range count and range search.
   ***************************************************************************/
   /**
   * Returns all keys in the symbol table as an Iterable.
   * To iterate over all of the keys in the symbol table named st,
   * use the foreach notation: for (Key key : st.keys()).
   * @return all keys in the symbol table as an Iterable
   */
   public Iterable<key> keys() {
     if (isEmpty()) {
       return new Queue<key>();
     }
     return keys(min(), max());
   }
   /**
   * Returns all keys in the symbol table in the given range,
   * as an Iterable.
   * @return all keys in the symbol table between lo 
   *  (inclusive) and hi (exclusive) as an Iterable
   * @throws NullPointerException if either lo or hi
   *  is null
   */
   public Iterable<key> keys(Key lo, Key hi) {
     if (lo == null) {
       throw new NullPointerException("first argument to keys() is null");
     }
     if (hi == null) {
       throw new NullPointerException("second argument to keys() is null");
     }
     Queue<key> queue = new Queue<key>();
     // if (isEmpty() || lo.compareTo(hi) > 0) return queue;
     keys(root, queue, lo, hi);
     return queue;
   } 
   // add the keys between lo and hi in the subtree rooted at x
   // to the queue
   private void keys(Node x, Queue<key> queue, Key lo, Key hi) { 
     if (x == null) {
       return; 
     }
     int cmplo = lo.compareTo(x.key); 
     int cmphi = hi.compareTo(x.key); 
     if (cmplo < 0) {
       keys(x.left, queue, lo, hi); 
     }
     if (cmplo <= 0 && cmphi >= 0) {
       queue.enqueue(x.key); 
     }
     if (cmphi > 0) {
       keys(x.right, queue, lo, hi); 
     }
   } 
   /**
   * Returns the number of keys in the symbol table in the given range.
   * @return the number of keys in the symbol table between lo 
   *  (inclusive) and hi (exclusive)
   * @throws NullPointerException if either lo or hi
   *  is null
   */
   public int size(Key lo, Key hi) {
     if (lo == null) {
       throw new NullPointerException("first argument to size() is null");
     }
     if (hi == null) {
       throw new NullPointerException("second argument to size() is null");
     }
     if (lo.compareTo(hi) > 0) {
       return 0;
     }
     if (contains(hi)) {
       return rank(hi) - rank(lo) + 1;
     }
     else {
       return rank(hi) - rank(lo);     
     }
   }
  /***************************************************************************
   * Check integrity of red-black tree data structure.
   ***************************************************************************/
   private boolean check() {
     if (!isBST())      System.out.println("Not in symmetric order");
     if (!isSizeConsistent()) System.out.println("Subtree counts not consistent");
     if (!isRankConsistent()) System.out.println("Ranks not consistent");
     if (!is23())       System.out.println("Not a 2-3 tree");
     if (!isBalanced())    System.out.println("Not balanced");
     return isBST() && isSizeConsistent() && isRankConsistent() && is23() && isBalanced();
   }
   // does this binary tree satisfy symmetric order?
   // Note: this test also ensures that data structure is a binary tree since order is strict
   private boolean isBST() {
     return isBST(root, null, null);
   }
   // is the tree rooted at x a BST with all keys strictly between min and max
   // (if min or max is null, treat as empty constraint)
   // Credit: Bob Dondero's elegant solution
   private boolean isBST(Node x, Key min, Key max) {
     if (x == null) {
       return true;
     }
     if (min != null && x.key.compareTo(min) <= 0) {
       return false;     
     }
     if (max != null && x.key.compareTo(max) >= 0) {
       return false;
     }
     return isBST(x.left, min, x.key) && isBST(x.right, x.key, max);
   } 
   // are the size fields correct?
   private boolean isSizeConsistent() { 
     return isSizeConsistent(root); 
   }
   private boolean isSizeConsistent(Node x) {
     if (x == null) {
       return true;
     }
     if (x.size != size(x.left) + size(x.right) + 1) {
       return false;
     }
     return isSizeConsistent(x.left) && isSizeConsistent(x.right);
   } 
   // check that ranks are consistent
   private boolean isRankConsistent() {
     for (int i = 0; i < size(); i++) {
       if (i != rank(select(i))) {
         return false;
       }
     }
     for (Key key : keys()) {
       if (key.compareTo(select(rank(key))) != 0) {
         return false;
       }
     }
     return true;
   }
   // Does the tree have no red right links, and at most one (left)
   // red links in a row on any path?
   private boolean is23() { 
     return is23(root); 
   }
   private boolean is23(Node x) {
     if (x == null) {
       return true;
     }
     if (isRed(x.right)) {
       return false;
     }
     if (x != root && isRed(x) && isRed(x.left)){
       return false;
     }
     return is23(x.left) && is23(x.right);
   } 
   // do all paths from root to leaf have same number of black edges?
   private boolean isBalanced() { 
     int black = 0;   // number of black links on path from root to min
     Node x = root;
     while (x != null) {
       if (!isRed(x)) black++;
       x = x.left;
     }
     return isBalanced(root, black);
   }
   // does every path from the root to a leaf have the given number of black links?
   private boolean isBalanced(Node x, int black) {
     if (x == null) {
       return black == 0;     
     }
     if (!isRed(x)) {
       black--;
     }
     return isBalanced(x.left, black) && isBalanced(x.right, black);
   } 
   /**
   * Unit tests the RedBlackBST data type.
   */
   public static void main(String[] args) { 
     RedBlackBST<string, integer=""> st = new RedBlackBST<string, integer="">();
     String data = "a b c d e f g h m n o p";
     Scanner sc = new Scanner(data);
     int i = 0;
     while (sc.hasNext()) {     
      String key = sc.next();
      st.put(key, i);
      i++;
     }
     sc.close();   
     for (String s : st.keys())
       System.out.println(s + " " + st.get(s));
     System.out.println();
     boolean result = st.check();
     System.out.println("check: " + result);
   }
 }

输出：

<code>a 0
b 1
c 2
d 3
e 4
f 5
g 6
h 7
m 8
n 9
o 10
p 11
 
check: true</code>

总结

以上就是本文关于java算法实现红黑树完整代码示例的全部内容，希望对大家有所帮助。感兴趣的朋友可以继续参阅本站：java集合中list的用法代码示例、Java微信支付之服务号支付代码示例、快速理解Java设计模式中的组合模式等，有什么问题可以随时留言，小编会及时回复大家的。感谢朋友们对本站的支持！