在python中画正态分布图像的实例

1.正态分布简介

正态分布(normal distribtution)又叫做高斯分布(Gaussian distribution)，是一个非常重要也非常常见的连续概率分布。正态分布大家也都非常熟悉，下面做一些简单的介绍。

假设随机变量XX服从一个位置参数为μμ、尺度参数为σσ的正态分布，则可以记为：

而概率密度函数为

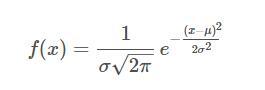
2.在python中画正态分布直方图

先直接上代码

import numpy as np
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt


def demo1():
  mu ,sigma = 0, 1
  sampleNo = 1000
  np.random.seed(0)
  s = np.random.normal(mu, sigma, sampleNo)

  plt.hist(s, bins=100, normed=True)
  plt.show()

上面是一个标准正态分布的直方图。最后输出的图像为：

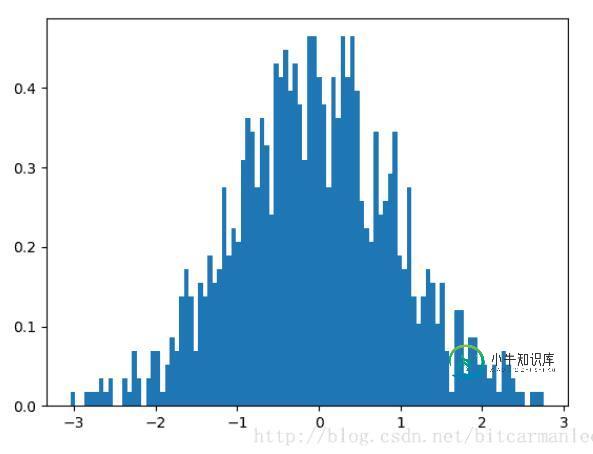
很多同学心里会有疑惑：这个图像看上去虽然是有点奇怪，虽然形状有点像正态分布，但是差得还比较多嘛，不能算是严格意义上的正态分布。

为什么会有这种情况出现呢？其实原因很简单，代码中我们设定的smapleno = 1000。这个数量并不是很大，所以整个图像看起来分布并不是很规则，只是有大致的正态分布的趋势。如果我们将这个参数加大，相当于增加样本数量，那么整个图像就会更加接近正态分布的形状。跟抛硬币的原理一致，抛的次数越多，正面与反面的出现概率更接近50%。

如果我们将sampleno设置为1000000，分布图像如下。

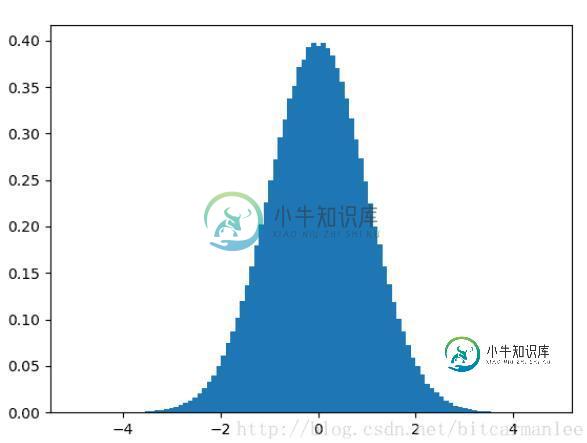
下面这个图像是不是看起来就漂亮多了！

3.画直方图与概率分布曲线

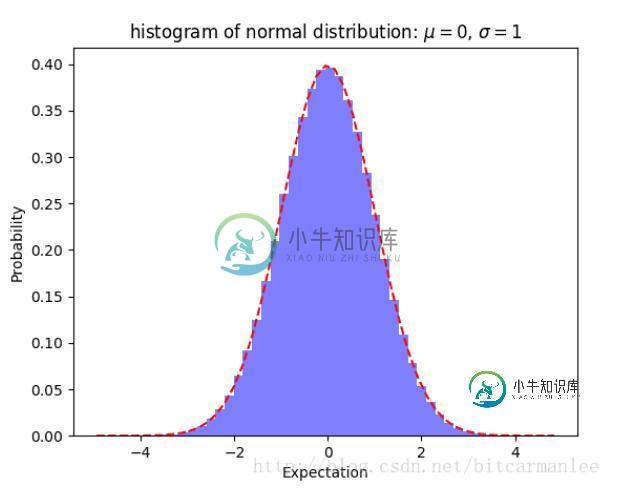
import numpy as np
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt

def demo2():
  mu, sigma , num_bins = 0, 1, 50
  x = mu + sigma * np.random.randn(1000000)
  # 正态分布的数据
  n, bins, patches = plt.hist(x, num_bins, normed=True, facecolor = 'blue', alpha = 0.5)
  # 拟合曲线
  y = mlab.normpdf(bins, mu, sigma)
  plt.plot(bins, y, 'r--')
  plt.xlabel('Expectation')
  plt.ylabel('Probability')
  plt.title('histogram of normal distribution: $\mu = 0$, $\sigma=1$')

  plt.subplots_adjust(left = 0.15)
  plt.show()

最后得到的图像为：

以上这篇在python中画正态分布图像的实例就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持小牛知识库。