迪菲－赫尔曼密钥交换(Diffie–Hellman)算法原理和PHP实现版

迪菲－赫尔曼(Diffie–Hellman)是一个可以让双方在不安全的公共信道上建立秘钥的一种算法，双方后期就可以利用这个秘钥加密(如RC4)内容。
迪菲－赫尔曼(Diffie–Hellman)算法原理很简单：

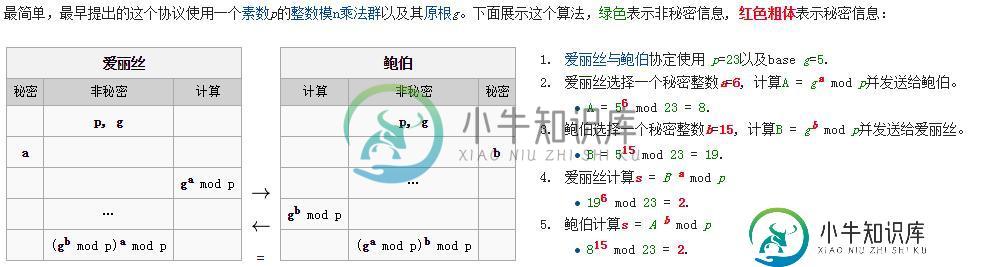
如上原理，最后很容易通过数学原理证明(g^b%p)^a%p = (g^a%p)^b%p，因此它们得到一个相同的密钥。
上面除了a,b和最后得出的公共密钥是秘密的，其它都是可以在公共信道上传递。实际运用中p很大(300位以上)，g通常取2或5。那么几乎不可能从p,g和g^a%p算出a(离散数学问题)。

很多语言都对该算法做了实现，以PHP package中Crypt_DiffieHellman为例：

<?php
include 'DiffieHellman.php';
 
/*
 *   Alice: prime = 563
 *       generator = 5
 *       private key = 9
 *   Bob:  prime = 563
 *       generator = 5
 *       private key = 14
 */
 
$p = 563;
$g = 5;
$alice = new Crypt_DiffieHellman($p, $g, 9);
$alice_pubKey = $alice->generateKeys()->getPublicKey();
 
$bob = new Crypt_DiffieHellman($p, $g, 14);
$bob_pubKey = $bob->generateKeys()->getPublicKey();
 
$alice_computeKey = $alice->computeSecretKey($bob_pubKey)->getSharedSecretKey();
$bob_computeKey = $bob->computeSecretKey($alice_pubKey)->getSharedSecretKey();
 
echo "{$alice_pubKey}-{$bob_pubKey}-{$alice_computeKey}-{$bob_computeKey}"; //78-534-117-117