解析C++哈夫曼树编码和译码的实现

一．背景介绍：

给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

二．实现步骤：

1.构造一棵哈夫曼树

2.根据创建好的哈夫曼树创建一张哈夫曼编码表

3.输入一串哈夫曼序列，输出原始字符

三．设计思想：

1.首先要构造一棵哈夫曼树，哈夫曼树的结点结构包括权值，双亲，左右孩子；假如由n个字符来构造一棵哈夫曼树，则共有结点2n-1个；在构造前，先初始化，初始化操作是把双亲，左右孩子的下标值都赋为0；然后依次输入每个结点的权值

2.第二步是通过n-1次循环，每次先找输入的权值中最小的两个结点，把这两个结点的权值相加赋给一个新结点，，并且这个新结点的左孩子是权值最小的结点，右孩子是权值第二小的结点；鉴于上述找到的结点都是双亲为0的结点，为了下次能正确寻找到剩下结点中权值最小的两个结点，每次循环要把找的权值最小的两个结点的双亲赋值不为0（i）.就这样通过n-1循环下、操作，创建了一棵哈夫曼树，其中，前n个结点是叶子（输入的字符结点）后n-1个是度为2的结点

 3.编码的思想是逆序编码，从叶子结点出发，向上回溯，如果该结点是回溯到上一个结点的左孩子，则在记录编码的数组里存“0”，否则存“1”，注意是倒着存；直到遇到根结点（结点双亲为0），每一次循环编码到根结点，把编码存在编码表中，然后开始编码下一个字符（叶子）

4．译码的思想是循环读入一串哈夫曼序列，读到“0”从根结点的左孩子继续读，读到“1”从右孩子继续，如果读到一个结点的左孩子和右孩子是否都为0，如果是说明已经读到了一个叶子（字符），翻译一个字符成功，把该叶子结点代表的字符存在一个存储翻译字符的数组中，然后继续从根结点开始读，直到读完这串哈夫曼序列，遇到结束符便退出翻译循环

四．源代码：

/***************************************
目的：1.根据输入的字符代码集及其权值集，
构造赫夫曼树，输出各字符的赫夫曼编码
2.输入赫夫曼码序列，输出原始字符代码
作者：Dmego  时间：2016-11-11
****************************************/
#include<iostream>
#define MAX_MA 1000
#define MAX_ZF 100
using namespace std;

//哈夫曼树的储存表示
typedef struct
{
 int weight; //结点的权值
 int parent, lchild, rchild;//双亲，左孩子，右孩子的下标
}HTNode,*HuffmanTree; //动态分配数组来储存哈夫曼树的结点
 
//哈夫曼编码表的储存表示
typedef char **HuffmanCode;//动态分配数组存储哈夫曼编码

//返回两个双亲域为0且权值最小的点的下标
void Select(HuffmanTree HT, int n, int &s1, int &s2)
{
 /*n代表HT数组的长度
 */

 //前两个for循环找所有结点中权值最小的点（字符）
 for (int i = 1; i <= n; i++)
 {//利用for循环找出一个双亲为0的结点
  if (HT[i].parent == 0)
  {
   s1 = i;//s1初始化为i
   break;//找到一个后立即退出循环
  }
 }
 for (int i = 1; i <= n; i++)
 {/*利用for循环找到所有结点（字符）权值最小的一个
  并且保证该结点的双亲为0*/
  if (HT[i].weight < HT[s1].weight && HT[i].parent == 0)
   s1 = i;
 }
 //后两个for循环所有结点中权值第二小的点（字符）
 for (int i = 1; i <= n; i++)
 {//利用for循环找出一个双亲为0的结点，并且不能是s1
  if (HT[i].parent == 0 && i != s1)
  {
   s2 = i;//s2初始化为i
   break;//找到一个后立即退出循环
  } 
 }

 for (int i = 1; i <= n; i++)
 {/*利用for循环找到所有结点（字符）权值第二小的一个，
  该结点满足不能是s1且双亲是0*/
  if (HT[i].weight < HT[s2].weight && HT[i].parent == 0 && i!= s1)
   s2 = i;
 }

}

//构造哈夫曼树
void CreateHuffmanTree(HuffmanTree &HT, int n)
{
/*-----------初始化工作-------------------------*/
 if (n <= 1)
  return;
 int m = 2 * n - 1;
 HT = new HTNode[m + 1];
 for (int i = 1; i <= m; ++i)
 {//将1~m号单元中的双亲，左孩子，右孩子的下标都初始化为0
  HT[i].parent = 0; HT[i].lchild = 0; HT[i].rchild = 0;
 }
 for (int i = 1; i <= n; ++i)
 {
  cin >> HT[i].weight;//输入前n个单元中叶子结点的权值
 }
/*-----------创建工作---------------------------*/
 int s1,s2;
 for (int i = n + 1; i <= m; ++i)
 {//通过n-1次的选择，删除，合并来构造哈夫曼树
  Select(HT, i - 1, s1, s2);
  /*cout << HT[s1].weight << " , " << HT[s2].weight << endl;*/
  /*将s1,s2的双亲域由0改为i
  (相当于把这两个结点删除了，这两个结点不再参与Select()函数)*/
  HT[s1].parent = i;
  HT[s2].parent = i;
  //s1,与s2分别作为i的左右孩子
  HT[i].lchild = s1;
  HT[i].rchild = s2;
  //结点i的权值为s1,s2权值之和
  HT[i].weight = HT[s1].weight + HT[s2].weight;
 }
}

//从叶子到根逆向求每个字符的哈夫曼编码，储存在编码表HC中
void CreatHuffmanCode(HuffmanTree HT, HuffmanCode &HC, int n)
{
 HC = new char*[n + 1];//分配储存n个字符编码的编码表空间
 char *cd = new char[n];//分配临时存储字符编码的动态空间
 cd[n - 1] = '\0';//编码结束符
 for (int i = 1; i <= n; i++)//逐个求字符编码
 {
  int start = n - 1;//start 开始指向最后，即编码结束符位置
  int c = i;
  int f = HT[c].parent;//f指向结点c的双亲
  while (f != 0)//从叶子结点开始回溯，直到根结点
  {
   --start;//回溯一次，start向前指向一个位置
   if (HT[f].lchild == c) cd[start] = '0';//结点c是f的左孩子，则cd[start] = 0;
   else cd[start] = '1';//否则c是f的右孩子，cd[start] = 1
   c = f;
   f = HT[f].parent;//继续向上回溯
  }
  HC[i] = new char[n - start];//为第i个字符编码分配空间
  strcpy(HC[i], &cd[start]);//把求得编码的首地址从cd[start]复制到HC的当前行中
 }
 delete cd;
}

//哈夫曼译码
void TranCode(HuffmanTree HT,char a[],char zf[],char b[],int n)
{
 /*
 HT是已经创建好的哈夫曼树
 a[]用来传入二进制编码
 b[]用来记录译出的字符
 zf[]是与哈夫曼树的叶子对应的字符（叶子下标与字符下标对应）
 n是字符个数，相当于zf[]数组得长度
 */

 int q = 2*n-1;//q初始化为根结点的下标
 int k = 0;//记录存储译出字符数组的下标
 int i = 0;
 for (i = 0; a[i] != '\0';i++)
 {//html" target="_blank">for循环结束条件是读入的字符是结束符（二进制编码）
  //此代码块用来判断读入的二进制字符是0还是1
  if (a[i] == '0')
  {/*读入0，把根结点(HT[q])的左孩子的下标值赋给q
   下次循环的时候把HT[q]的左孩子作为新的根结点*/
   q = HT[q].lchild;
  }
  else if (a[i] == '1')
  {
   q = HT[q].rchild;
  }
  //此代码块用来判断HT[q]是否为叶子结点
  if (HT[q].lchild == 0 && HT[q].rchild == 0)
  {/*是叶子结点，说明已经译出一个字符
  该字符的下标就是找到的叶子结点的下标*/
   b[k++] = zf[q];//把下标为q的字符赋给字符数组b[]
   q = 2 * n - 1;//初始化q为根结点的下标
   //继续译下一个字符的时候从哈夫曼树的根结点开始
  }
 }
 /*译码完成之后，用来记录译出字符的数组由于没有结束符输出的
 时候回报错，故紧接着把一个结束符加到数组最后*/
 b[k] = '\0';
}
//菜单函数
void menu()
{
 cout << endl;
 cout << "  ┏〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓┓" << endl;
 cout << "  ┃  ★★★★★★★哈夫曼编码与译码★★★★★★★  ┃" << endl;
 cout << "  ┃     1. 创建哈夫曼树      ┃" << endl;
 cout << "  ┃     2. 进行哈夫曼编码      ┃" << endl;
 cout << "  ┃     3. 进行哈夫曼译码      ┃" << endl;
 cout << "  ┃     4. 退出程序       ┃" << endl;
 cout << "  ┗〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓┛" << endl;
 cout << "      <><注意：空格字符用'- '代替><>" << endl;
 cout << endl;
}
void main()
{
 int falg;//记录要编码的字符个数
 char a[MAX_MA];//储存输入的二进制字符
 char b[MAX_ZF];//存储译出的字符
 char zf[MAX_ZF];//储存要编码的字符
 HuffmanTree HT = NULL;//初始化树为空数
 HuffmanCode HC = NULL;//初始化编码表为空表
 menu();
 while (true)
 {
  int num;
  cout << "<><请选择功能(1-创建 2-编码 3-译码 4-退出)><>: ";
   cin >> num;
   switch (num)
   {
   case 1 :
    cout << "<><请输入字符个数><>:";
    cin >> falg;
    //动态申请falg个长度的字符数组，用来存储要编码的字符
    /*char *zf = new char[falg];*/
    cout << "<><请依次输入" << falg << "个字符:><>: ";
    for (int i = 1; i <= falg; i++)
     cin >> zf[i];
    cout << "<><请依次输入" << falg << "个字符的权值><>: ";
    CreateHuffmanTree(HT, falg);//调用创建哈夫曼树的函数
    cout << endl;
    cout << "<><创建哈夫曼成功！,下面是该哈夫曼树的参数输出><>：" << endl;
    cout << endl;
    cout << "结点i"<<"\t"<<"字符" << "\t" << "权值" << "\t" << "双亲" << "\t" << "左孩子" << "\t" << "右孩子" << endl;
    for (int i = 1; i <= falg * 2 - 1; i++)
    {
     cout << i << "\t"<<zf[i]<< "\t" << HT[i].weight << "\t" << HT[i].parent << "\t" << HT[i].lchild << "\t" << HT[i].rchild << endl;
    }
    cout << endl;
    break;
   case 2:
    CreatHuffmanCode(HT, HC, falg);//调用创建哈夫曼编码表的函数
    cout << endl;
    cout << "<><生成哈夫曼编码表成功！,下面是该编码表的输出><>：" << endl;
    cout << endl;
    cout << "结点i"<<"\t"<<"字符" << "\t" << "权值" << "\t" << "编码" << endl;
    for (int i = 1; i <= falg; i++)
    {
     cout << i << "\t"<<zf[i]<< "\t" << HT[i].weight << "\t" << HC[i] << endl;
    }
    cout << endl;
    break;
   case 3:
    cout << "<><请输入想要翻译的一串二进制编码><>：";
    /*这样可以动态的直接输入一串二进制编码，
    因为这样输入时最后系统会自动加一个结束符*/
    cin >> a;
    TranCode(HT, a, zf, b, falg);//调用译码的函数，
     /*这样可以直接把数组b输出，因为最后有
     在数组b添加输出时遇到结束符会结束输出*/
    cout << endl;
    cout << "<><译码成功！翻译结果为><>：" << b << endl;
    cout << endl;
    break;
   case 4:
    cout << endl;
    cout << "<><退出成功！><>" << endl;
    exit(0);
   default:
    break;
   }
 }
 
 //-abcdefghijklmnopqrstuvwxyz
 //186 64 13 22 32 103 21 15 47 57 1 5 32 20 57 63 15 1 48 51 80 23 8 18 1 16 1
 //000101010111101111001111110001100100101011110110

}

五．运行截图：

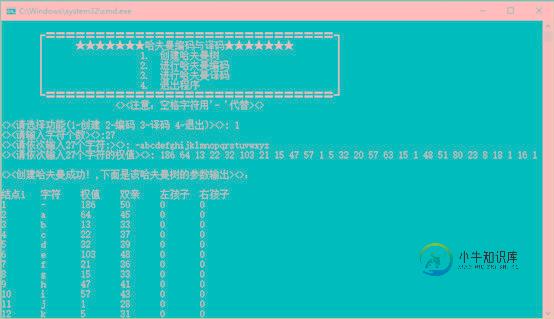
原文链接：http://www.cnblogs.com/dmego/p/6064069.html

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持小牛知识库。