python seaborn heatmap可视化相关性矩阵实例
方法
import pandas as pd import numpy as np import seaborn as sns df = pd.DataFrame(np.random.randn(50).reshape(10,5)) corr = df.corr() sns.heatmap(corr, cmap='Blues', annot=True)
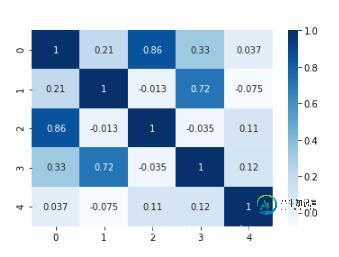
将矩阵型简化为对角矩阵型:
mask = np.zeros_like(corr) mask[np.tril_indices_from(mask)] = True sns.heatmap(corr, cmap='Blues', annot=True, mask=mask.T)
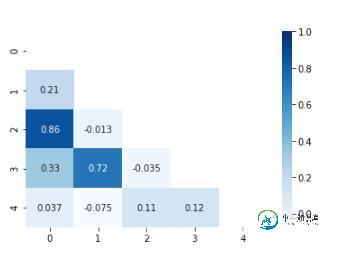
补充知识:Python【相关矩阵】和【协方差矩阵】
相关系数矩阵
pandas.DataFrame(数据).corr()
import pandas as pd
df = pd.DataFrame({
'a': [11, 22, 33, 44, 55, 66, 77, 88, 99],
'b': [10, 24, 30, 48, 50, 72, 70, 96, 90],
'c': [91, 79, 72, 58, 53, 47, 34, 16, 10],
'd': [99, 10, 98, 10, 17, 10, 77, 89, 10]})
df_corr = df.corr()
# 可视化
import matplotlib.pyplot as mp, seaborn
seaborn.heatmap(df_corr, center=0, annot=True, cmap='YlGnBu')
mp.show()
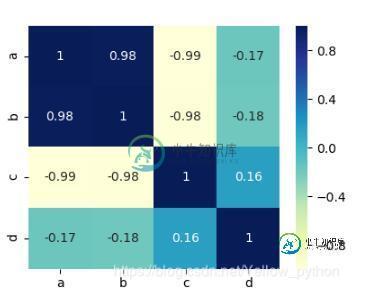
协方差矩阵
numpy.cov(数据)
import numpy as np matric = [ [11, 22, 33, 44, 55, 66, 77, 88, 99], [10, 24, 30, 48, 50, 72, 70, 96, 90], [91, 79, 72, 58, 53, 47, 34, 16, 10], [55, 20, 98, 19, 17, 10, 77, 89, 14]] covariance_matrix = np.cov(matric) # 可视化 print(covariance_matrix) import matplotlib.pyplot as mp, seaborn seaborn.heatmap(covariance_matrix, center=0, annot=True, xticklabels=list('abcd'), yticklabels=list('ABCD')) mp.show()
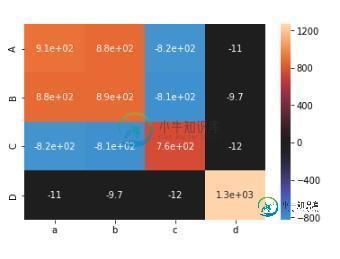
补充
协方差
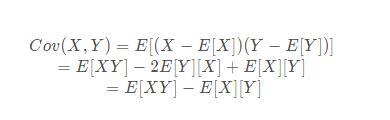
相关系数
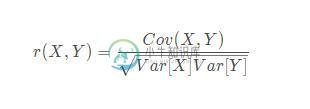
EXCEL也能做
CORREL函数
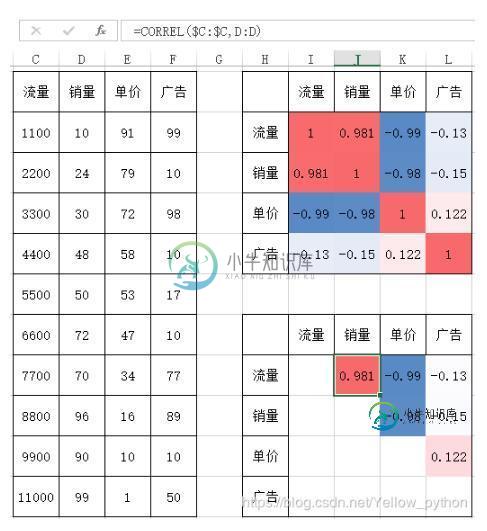
以上这篇python seaborn heatmap可视化相关性矩阵实例就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持小牛知识库。
-
本章节主要给大家引入视图矩阵和投影矩阵两个新的概念,如果你没有图形学基础,对这两个概念暂时还没有认知,也没有关系。通过前面的学习相信你对平移、旋转等矩阵有了一定的认知,至于投影和视图矩阵和平移、旋转等模型矩阵一样也会对WebGL顶点进行坐标变换,至于如何变换下面会逐步讲解。 在学习本章节之前,如果你对Three.js已经有了一定的了解,可以尝试从WebGL视图矩阵和投影矩阵的角度去深入理解Thre
-
主要内容:可追溯性矩阵的目标可追踪性矩阵是一种表格类型的文档,用于开发软件应用程序以跟踪需求。它可用于向前(从需求到设计或编码)和向后(从编码到需求)跟踪。它也称为需求可追踪性矩阵(RTM)。 通常,这就像一个包含表格的工作表文档,但是还有许多用户定义的可追溯性矩阵模板。可追溯性矩阵中的每个要求都与其各自的测试用例相关联,以便可以根据具体要求顺序执行测试。 下面给出一个表作为示例,以便可以理解可追溯性矩阵的格式: 业务需求
-
Many datasets contain multiple quantitative variables, and the goal of an analysis is often to relate those variables to each other. We regplot() and lmplot() are closely related, and share much of th
-
如何计算大的皮尔逊互相关矩阵( 更新:我读了阿帕奇火花的实现 但对我来说,看起来所有的计算都发生在一个节点上,而不是真正意义上的分布式。 请在这里放一些光。我还尝试在3节点火花群集上执行它,下面是屏幕截图: 正如您从第二张图中看到的,数据在一个节点上被拉起,然后进行计算。我在这里对吗?
-
我有两个列表,每个列表中有两个矩阵。。是否有一种方法可以对它们进行矩阵计算,即相加,其中matrix1中的蓝色矩阵与matrix2中的蓝色矩阵相加,matrix1中的红色矩阵与matrix2中的红色矩阵相加。我能想到的唯一方法是在循环中进行计算 请注意,我将有大约10个,以及不止一组(即蓝色、红色、绿色、紫色)
-
问题内容: 我正在使用阴影中的形状生成使用安装在移动平台上的相机拍摄的图像的数字地形模型(DTM)。用Python编写的算法似乎运行得很好,但是输出是倾斜的并且有点球形,所以我怀疑我需要从DTM中消除透视失真和桶形。 如果有人对此感兴趣,可以在这里获得数据。 摄像机以41度倾斜安装,并具有以下摄像机和失真矩阵: 如何应用透视变换并从此矩阵中消除桶形失真以获得平坦的DTM? 我已经尝试过使用Open

