在Javascript AVL树中计算平衡因子
AVL树检查左子树和右子树的高度,并确保差异不超过1。该差异称为“平衡因子”。
例如,在以下树中,第一棵树是平衡的,接下来的两棵树是不平衡的-
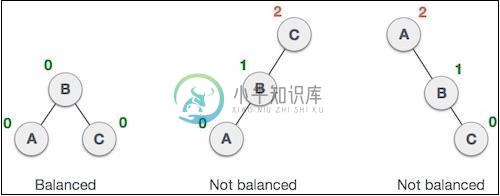
在第二棵树中,C的左子树的高度为2,而右边子树的高度为0,所以差为2。在第三棵树中,A的右子树的高度为2,而左子树的高度为2,所以它为0。 ,并且相差再次为2。AVL树允许差异(平衡因子)仅为1。
BalanceFactor = height(left-sutree) − height(right-sutree)
如果左右子树的高度差大于1,则使用某些旋转技术来平衡树。
让我们定义此方法并初始化类-
示例
class AVLTree {
constructor() {
//将根元素初始化为null。
this.root = null;
}
getBalanceFactor(root) {
return this.getHeight(root.left) - this.getHeight(root.right);
}
getHeight(root) {
let height = 0;
if (root === null) {
height = -1;
} else {
height = Math.max(this.getHeight(root.left), this.getHeight(root.right)) + 1;
}
return height;
}
}
AVLTree.prototype.Node = class {
constructor(data, left = null, right = null) {
this.data = data;
this.left = left;
this.right = right;
}
};
-
AVL树是一种平衡的二元搜索树,即高度=O(log(n))。这是通过确保每个节点都遵循AVL树属性来实现的: 左侧子树(LST)的高度-右侧子树(RST)的高度在[-1,0,1]范围内 其中,对于给定节点,高度(LST)-高度(RST)称为平衡因子(BF)。 根据这个定义,叶子的高度是0。但是几乎每次讨论AVL树时,人们都认为叶子的高度是1。 我的问题是,我们能把叶子的高度取为0吗?这将使以下BS
-
我正在解决“破解编码面试”中的以下问题:实现一个函数来检查二叉树是否平衡。平衡树是这样一种树:任何节点的两个子树的高度相差不会超过一个。 这本书的示例解决方案(复制如下)假设从节点发出的树是平衡的,如果(a)节点的左子树和右子树是平衡的;和(b)节点本身是平衡的。我在试图理解为什么会这样?以上两个条件的满足如何证明从节点发出的整个树是平衡的? 谢啦
-
我目前正在编写一个递归方法,以返回整个二元搜索树上的最大不平衡。我对递归编程非常陌生,所以很难理解。我构建的树的不平衡度为1,但我的方法只返回0。我相信我的逻辑是有缺陷的。 我百分之百确定它正在运行“(root==null){返回0;}”在方法的每个步骤中。我尝试删除它并进一步定义它,它仍在继续这样做。 这是我当前的方法:
-
主要内容:二叉排序树转化为平衡二叉树,构建平衡二叉树的代码实现,总结上一节介绍如何使用二叉排序树实现动态 查找表,本节介绍另外一种实现方式—— 平衡二叉树。 平衡二叉树,又称为 AVL 树。实际上就是遵循以下两个特点的二叉树: 每棵子树中的左子树和右子树的深度差不能超过 1; 二叉树中每棵子树都要求是平衡二叉树; 其实就是在二叉树的基础上,若树中每棵子树都满足其左子树和右子树的深度差都不超过 1,则这棵二叉树就是平衡二叉树。 图 1 平衡与不平衡的二叉树及结点的
-
给定一棵仅由加减法运算符、数字组成的二进制算术表达式树,如何使树尽可能平衡?任务是在不求表达式值的情况下平衡树,即节点数应该保持不变。 示例: 加法是可交换的和相联的,这允许平衡。交换性允许交换连续“+”节点的子节点。关联性允许旋转。在上述示例中,所执行的转换可以被视为 null 另一种方法可以是将表达式树读入数组,并用变量替换任何'-'子树。然后使用DP确定括号的最佳位置。这必须是自下而上的,这
-
我正在解决LeetCode问题110。平衡二叉树: 给定一棵二叉树,确定它是否是高度平衡的。 对于这个问题,高度平衡的二叉树定义为: 一种二叉树,其中每个节点的左右子树的高度相差不超过1。 我已经看到了这个问题的解决方案,包括这个: 我的问题是:为什么要添加此代码? 当我从代码中删除它时,它看起来工作得很好。但是,当测试用例为< code>[1,2,2,3,null,null,3,4,null,n

