《关于秋招我想说》专题
-
关于 MongoDump 和 MongoRestore
MongoDB 提供了两个用于备份和还原操作的实用工具：MongoDump 和 MongoRestore。它们对于创建小型数据库的备份和还原数据非常有用。
-
关于仪表板
仪表板是图表的集合，可让你创建和查看数据可视化。当你修改图表时，包含该图表的所有仪表板都将反映所做的更改。 页面窗格 页面窗格显示仪表板中每个页面的缩略图。如果页面窗格已隐藏，从菜单栏选择“查看”->“显示页面”。 仪表板工具栏 仪表板工具栏提供可用于刷新数据和显示仪表板的控件。 控件列表窗格 控件列表窗格让你设计仪表板，例如添加图表、标签、图像。如果控件列表窗格已隐藏，从菜单栏选择“查看”->“
-
关于数据源
数据源引用连接中的表，并且可以从不同服务器类型的表中选择数据。数据集中的字段可用于构造图表。在构建图表时，你需要指定图表使用的数据源。 连接窗格 连接窗格是浏览连接、数据库、表、查询的基本途径。如果连接窗格已隐藏，从菜单栏选择“查看”->“显示连接”。 数据源工具栏 数据源工具栏提供了可用于处理数据的控件。 设计窗格 设计窗格让你直观地构建数据源。 Navicat 提供了两种用于连接数据的模式：实
-
关于 MongoImport 和 MongoExport
MongoDB 为导入和导出数据提供了两个实用工具：MongoImport 和 MongoExport。你可以根据指定的条件导入或导出数据。
-
关于 MongoDump 和 MongoRestore
MongoDB 提供了两个用于备份和还原操作的实用工具：MongoDump 和 MongoRestore。它们对于创建小型数据库的备份和还原数据非常有用。
-
关于仪表板
仪表板是图表的集合，可让你创建和查看数据可视化。当你修改图表时，包含该图表的所有仪表板都将反映所做的更改。 页面窗格 页面窗格显示仪表板中每个页面的缩略图。如果页面窗格已隐藏，从菜单栏选择“查看”->“显示页面”。 仪表板工具栏 仪表板工具栏提供可用于刷新数据和显示仪表板的控件。 控件列表窗格 控件列表窗格让你设计仪表板，例如添加图表、标签、图像。如果控件列表窗格已隐藏，从菜单栏选择“查看”->“
-
关于数据源
数据源引用连接中的表，并且可以从不同服务器类型的表中选择数据。数据集中的字段可用于构造图表。在构建图表时，你需要指定图表使用的数据源。 连接窗格 连接窗格是浏览连接、数据库、表、查询的基本途径。如果连接窗格已隐藏，从菜单栏选择“查看”->“显示连接”。 数据源工具栏 数据源工具栏提供了可用于处理数据的控件。 设计窗格 设计窗格让你直观地构建数据源。 Navicat 提供了两种用于连接数据的模式：实
-
关于 MongoImport 和 MongoExport
MongoDB 为导入和导出数据提供了两个实用工具：MongoImport 和 MongoExport。你可以根据指定的条件导入或导出数据。
-
关于 MongoDump 和 MongoRestore
MongoDB 提供了两个用于备份和还原操作的实用工具：MongoDump 和 MongoRestore。它们对于创建小型数据库的备份和还原数据非常有用。
-
关于仪表板
仪表板是图表的集合，可让你创建和查看数据可视化。当你修改图表时，包含该图表的所有仪表板都将反映所做的更改。 页面窗格 页面窗格显示仪表板中每个页面的缩略图。如果页面窗格已隐藏，从菜单栏选择“查看”->“显示页面”。 仪表板工具栏 仪表板工具栏提供可用于刷新数据和显示仪表板的控件。 控件列表窗格 控件列表窗格让你设计仪表板，例如添加图表、标签、图像。如果控件列表窗格已隐藏，从菜单栏选择“查看”->“
-
关于数据源
数据源引用连接中的表，并且可以从不同服务器类型的表中选择数据。数据集中的字段可用于构造图表。在构建图表时，你需要指定图表使用的数据源。 连接窗格 连接窗格是浏览连接、数据库、表、查询的基本途径。如果连接窗格已隐藏，从菜单栏选择“查看”->“显示连接”。 数据源工具栏 数据源工具栏提供了可用于处理数据的控件。 设计窗格 设计窗格让你直观地构建数据源。 Navicat 提供了两种用于连接数据的模式：实
-
关于 MongoImport 和 MongoExport
MongoDB 为导入和导出数据提供了两个实用工具：MongoImport 和 MongoExport。你可以根据指定的条件导入或导出数据。
-
我有一个关于cs50中潮汐问题的问题
我在pset3(cs50)中做tideman问题，但是我不能区分我的程序和函数look_pairs的正确程序之间的区别。 这是我的程序，我在正确的程序之间做了一点区别。我没有判断makeCycle（winner,I）的返回，而是返回这个函数，你可以在我的代码中看到区别。 这是正确的版本，但我认为我的程序和正确的版本是一样的，我不知道为什么我的程序会造成这个错误。
-
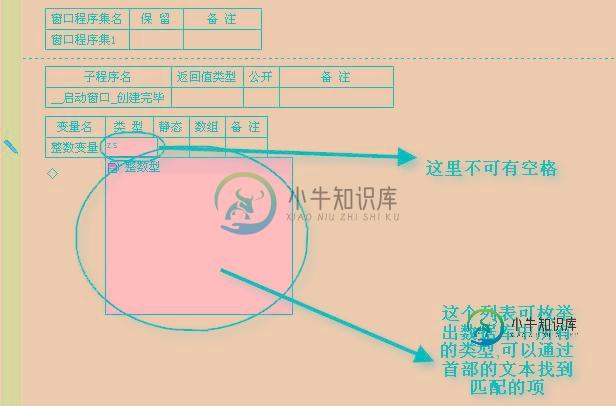一步一步跟我学易语言之关于变量本文向大家介绍一步一步跟我学易语言之关于变量，包括了一步一步跟我学易语言之关于变量的使用技巧和注意事项，需要的朋友参考一下 下面来介绍变量相关的知识。 什么是变量？ 顾名思义变量就是一种自身可改变值的可使用的虚拟的质体。简单的说把变量比作一个盒子，当你的东西需要保存时这个盒子派上了用场把你想要存放的东西放到盒子里，如果需要用盒子里的东西就把东西拿出来不需要时再放回去，或这里的部分或全部的不需要了就
-
关于中位数算法的中位数，我不了解
关于中位数的算法，有一点我不明白。这个算法的一个关键步骤是找到一个近似的中位数，根据维基百科，我们保证这个近似的中位数大于初始集元素的30%。 为了找到这个近似中位数，我们计算每组5个元素的中位数，将这些中位数聚集在一个新的集合中，然后重新计算中位数，直到获得的集合至少包含5个元素。在这种情况下，我们得到集合的中值。（如果我的解释不清楚，请参阅维基百科页面。） 但是，请考虑以下125个元素: 因此