合并附近的多边形

Question

我有一对（封闭的）多边形，每个多边形被定义为一个点序列（顶点）。每个多边形都代表一块土地，由一条小河分开，所以溪流在两个多边形之间形成一个狭窄的缝隙。

我正在寻找一种算法，通过将两个多边形连接成一个连接的多边形来识别和消除间隙。

下图显示了一个示例，其中原始多边形为绿色和红色，生成的多边形显示为黄色。

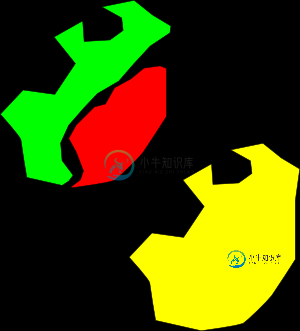
到目前为止，我已经能够做到以下几点：

• 对于多边形A中的每条边，找到多边形B中最近的顶点。
• 找到多边形-B与多边形-a之间一定距离内的所有顶点

但我不确定我现在需要做什么。

Answer 1

你可以试试形态学手术。具体来说，你可以尝试扩张，然后侵蚀（也称为形态学“闭合”）。放大n个像素——其中n大于河流的宽度——将组合这些形状。随后的侵蚀会消除对图形其余部分造成的大部分损坏。这不是完美的（它会完美地结合这两种形状，但以牺牲图形其余部分的一些软化为代价），但也许通过整体操作的结果，你可以找到一种方法来纠正它。

一般来说，这些形态学操作是在位图上完成的，而不是在多边形上。但是在多边形的角上运行简单的操作可能行得通。

Answer 2

你可以看看凸壳算法的改进。凸包算法获取一组点，并绘制包含这些点的最小凸面形状。你的问题几乎是一个凸包问题，除了顶部的凹面区域。简单地使用凸包算法就可以得到这个结果，虽然很接近，但并不是你所需要的（注意，棕色区域是不同的）

根据你想要做的，凸包可能“足够好”，但是如果没有，你仍然可以修改一个算法来忽略非凸包的部分，然后simpy合并两个多边形。

具体来说，这张pdf展示了如何合并两个凸面外壳，这与您正在尝试的非常相似。

Answer 3

为了完整起见，我想分享我的解决方案，作为一个python实现。这是基于Retsam的公认答案，以及David Eisenstat在该答案的评论中提出的想法，即用该多边形的中间顶点替换连接到同一原始多边形顶点的凸包上的边。

def joinPolygons(polya, polyb):
    """
    Generate and return a single connected polygon which includes the two given
    polygons. The connection between the two polygons is based on the convex hull
    of the composite polygon. All polygons are sequences of two-tuples giving the
    vertices of the polygon as (x, y), in order. That means vertices that are adjacent
    in the sequence are adjacent in the polygon (connected by an edge). The first and
    last vertices in the sequence are also connected by any edge (implicitly closed, do
    not duplicate the first point at the end of the sequence to close it).

    Only simple polygons are supported (no self-intersection).
    """

    #Just to make it easier to identify and access by index.
    polygons = [polya, polyb]

    #Create a single list of points to create the convex hull for (each
    # point is a vertex of one of the polygons).
    #Additionally, each point includes some additional "cargo", indicating which
    # polygon it's from, and it's index into that polygon
    # This assumes the implementation of convexHull simply ignores everything
    # beyond the first two elements of each vertex.
    composite = []
    for i in range(len(polygons)):
        points = polygons[i]
        composite += [(points[j][0], points[j][1], j, i) for j in xrange(len(points))]

    #Get the convex hull of the two polygons together.
    ch = convexHull(composite)

    #Now we're going to walk along the convex hull and find edges that connect two vertices
    # from the same source polygon. We then replace that edge with all the intervening edges
    # from that source polygon.

    #Start with the first vertex in the CH.
    x, y, last_vnum, last_pnum = ch[0]

    #Here is where we will collect the vertices for our resulting polygon, starting with the
    # first vertex on the CH (all the vertices on the CH will end up in the result, plus some
    # additional vertices from the original polygons).
    results = [(x, y)]

    #The vertices of the convex hull will always walk in a particular direction around each
    # polygon (i.e., forwards in the sequence of vertices, or backwards). We will use this
    # to keep track of which way they go.
    directions = [None for poly in polygons]

    #Iterate over all the remaining points in the CH, and then back to the first point to
    # close it.
    for x, y, vnum, pnum in list(ch[1:]) + [ch[0]]:

        #If this vertex came from the same original polygon as the last one, we need to
        # replace the edge between them with all the intervening edges from that polygon.
        if pnum == last_pnum:

            #Number of vertices in the polygon
            vcount = len(polygons[pnum])

            #If an edge of the convex hull connects the first and last vertex of the polygon,
            # then the CH edge must also be an edge of the polygon, because the two vertices are
            # adjacent in the original polygon. Therefore, if the convex
            # hull goes from the first vertex to the last in a single edge, then it's walking
            # backwards around the polygon. Likewise, if it goes from the last to the first in 
            # a single edge, it's walking forwards.
            if directions[pnum] is None:
                if last_vnum < vnum:
                    if last_vnum == 0 and vnum == vcount - 1:
                        direction = -1
                    else:
                        direction = 1
                else:
                    if last_vnum == vcount - 1 and vnum == 0:
                        direction = 1
                    else:
                        direction = -1
                directions[pnum] = direction
            else:
                direction = directions[pnum]

            #Now walk from the previous vertex to the current one on the source
            # polygon, and add all the intevening vertices (as well as the current one
            # from the CH) onto the result.
            v = last_vnum
            while v != vnum:
                v += direction
                if v >= vcount:
                    v = 0
                elif v == -1:
                    v = vcount - 1
                results.append(polygons[pnum][v])

        #This vertex on the CH is from a different polygon originally than the previous
        # vertex, so we just leave them connected.
        else:
            results.append((x, y))

        #Remember this vertex for next time.
        last_vnum = vnum
        last_pnum = pnum

    return results



def convexHull(points, leftMostVert=None):
    """
    Returns a new polygon which is the convex hull of the given polygon.

    :param: leftMostVert    The index into points of the left most vertex in the polygon.
                            If you don't know what it is, pass None and we will figure it
                            out ourselves.
    """
    point_count = len(points)

    #This is implemented using the simple Jarvis march "gift wrapping" algorithm.
    # Generically, to find the next point on the convex hull, we find the point
    # which has the smallest clockwise-angle from the previous edge, around the
    # last point. We start with the left-most point and a virtual vertical edge
    # leading to it.

    #If the left-most vertex wasn't specified, find it ourselves.
    if leftMostVert is None:
        minx = points[0][0]
        leftMostVert = 0
        for i in xrange(1, point_count):
            x = points[i][0]
            if x < minx:
                minx = x
                leftMostVert = i

    #This is where we will build up the vertices we want to include in the hull.
    # They are stored as indices into the sequence `points`.
    sel_verts = [leftMostVert]

    #This is information we need about the "last point" and "last edge" in order to find
    # the next point. We start with the left-most point and a pretend vertical edge.

    #The index into `points` of the last point.
    sidx = leftMostVert

    #The actual coordinates (x,y) of the last point.
    spt = points[sidx]

    #The vector of the previous edge.
    # Vectors are joined tail to tail to measure angle, so it
    # starts at the last point and points towards the previous point.
    last_vect = (0, -1, 0)
    last_mag = 1.0

    #Constant
    twopi = 2.0*math.pi

    #A range object to iterate over the vertex numbers.
    vert_nums = range(point_count)

    #A list of indices of points which have been determined to be colinear with
    # another point and a selected vertex on the CH, and which are not endpoints
    # of the line segment. These points are necessarily not vertices of the convex
    # hull: at best they are internal to one of its edges.
    colinear = []

    #Keep going till we come back around to the first (left-most) point.
    while True:
        #Try all other end points, find the one with the smallest CW angle.
        min_angle = None
        for i in vert_nums:

            #Skip the following points:
            # -The last vertex (sidx)
            # -The second to last vertex (sel_verts[-2]), that would just backtrack along
            #  the edge we just created.
            # -Any points which are determined to be colinear and internal (indices in `colinear`).
            if i == sidx or (len(sel_verts) > 1 and i == sel_verts[-2]) or i in colinear:
                continue

            #The point to test (x,y)
            pt = points[i]

            #vector from current point to test point.
            vect = (pt[0] - spt[0], pt[1] - spt[1], 0)
            mag = math.sqrt(vect[0]*vect[0] + vect[1]*vect[1])

            #Now find clockwise angle between the two vectors. Start by
            # finding the smallest angle between them, using the dot product.
            # Then use cross product and right-hand rule to determine if that
            # angle is clockwise or counter-clockwise, and adjust accordingly.

            #dot product of the two vectors.
            dp = last_vect[0]*vect[0] + last_vect[1]*vect[1]
            cos_theta = dp / (last_mag * mag)

            #Ensure fp erros don't become domain errors.
            if cos_theta > 1.0:
                cos_theta = 1.0
            elif cos_theta < -1.0:
                cos_theta = -1.0

            #Smaller of the two angles between them.
            theta = math.acos(cos_theta)

            #Take cross product of last vector by test vector.
            # Except we know that Z components in both input vectors are 0,
            # So the X and Y components of the resulting vector will be 0. Plus,
            # we only care aboue the Z component of the result.
            cpz = last_vect[0]*vect[1] - last_vect[1]*vect[0]

            #Assume initially that angle between the vectors is clock-wise.
            cwangle = theta
            #If the cross product points up out of the plane (positive Z),
            # then the angle is actually counter-clockwise.
            if cpz > 0:
                cwangle = twopi - theta

            #If this point has a smaller angle than the others we've considered,
            # choose it as the new candidate.
            if min_angle is None or cwangle < min_angle:
                min_angle = cwangle
                next_vert = i
                next_mvect = vect
                next_mag = mag
                next_pt = pt

            #If the angles are the same, then they are colinear with the last vertex. We want
            # to pick the one which is furthest from the vertex, and put all other colinear points
            # into the list so we can skip them in the future (this isn't just an optimization, it
            # appears to be necessary, otherwise we will pick one of the other colinear points as
            # the next vertex, which is incorrect).
            #Note: This is fine even if this turns out to be the next edge of the CH (i.e., we find
            # a point with a smaller angle): any point with is internal-colinear will not be a vertex
            # of the CH.
            elif cwangle == min_angle:
                if mag > next_mag:
                    #This one is further from the last vertex, so keep it as the candidate, and put the
                    # other colinear point in the list.
                    colinear.append(next_vert)
                    min_angle = cwangle
                    next_vert = i
                    next_mvect = vect
                    next_mag = mag
                    next_pt = pt
                else:
                    #This one is closer to the last vertex than the current candidate, so just keep that
                    # as the candidate, and put this in the list.
                    colinear.append(i)

        #We've found the next vertex on the CH.
        # If it's the first vertex again, then we're done.
        if next_vert == leftMostVert:
            break
        else:
            #Otherwise, add it to the list of vertices, and mark it as the
            # last vertex.
            sel_verts.append(next_vert)
            sidx = next_vert
            spt = next_pt
            last_vect = (-next_mvect[0], -next_mvect[1])
            last_mag = next_mag

    #Now we have a list of vertices into points, but we really want a list of points, so
    # create that and return it.
    return tuple(points[i] for i in sel_verts)