坚持使用最小最大值算法 - 下一步是什么？哈斯克尔

Question

我正在为一个2人棋盘游戏编写一个基本的MiniMax算法。到目前为止，我有一个函数，它评估一个板并返回一个分数。我有一个函数，它将所有可能的移动（以及这些移动的移动）等的玫瑰树返回到给定的深度。我可以找到那棵树的叶子，并根据我的启发给它们一个值，我的问题是，在那之后我该怎么办？

我是否以某种方式编辑叶子的父节点，并根据子节点的值给父节点分配一个新值，然后继续下去，直到到达根节点？

我是否要从叶子向上创建一棵新树，选择最小值/最大值直到到达根节点？如果是这样，新树如何记住到达叶子所需的所有动作？

我只想使用标准库的导入（我不想下载包）。任何建议都很好，已经挣扎了几天了。谢谢

我试图挑选代码的某些部分来举例，但有很多函数纠缠在一起。如果它有帮助，这里是主要函数的类型签名和它们的作用的解释：

此函数接受Int（表示树的深度>）、 （棋盘的当前状态）、立即可能的移动列表，并返回玫瑰树，其中包含每个可能的移动（以及移动到这些移动）以及与该移动相关的分数。如果玩家是黑暗的，则其得分为正，如果玩家是暗的，则得分为负-玫瑰树中的每个深度都是玩家的下一步。

roseTreeAtDepthN :: Int-> Game -> [Position] -> [Rose (Position,score)]

例如：treeAtDepthN 2 initialGame [（2，3），（3，2），（4，5），（5，4）] 返回：

[Rose ((2,3),4) [Rose ((2,2),-3) [],Rose ((2,4),-3) [],Rose ((4,2),-3) []],
 Rose ((3,2),4) [Rose ((2,2),-3) [],Rose ((2,4),-3) [],Rose ((4,2),-3) []],
 Rose ((4,5),4) [Rose ((3,5),-3) [],Rose ((5,3),-3) [],Rose ((5,5),-3) []],
 Rose ((5,4),4) [Rose ((3,5),-3) [],Rose ((5,3),-3) [],Rose ((5,5),-3) []]]

我还有另一个功能，可以让我得到树的叶子。我使用treeAtDepthN中的函数来计算每次移动的游戏状态，但我意识到这可能不是必需的，应该只在树的叶子上使用。我不确定这是否有帮助。

稍后编辑：

不确定我的最小极大算法下一步该做什么。我有一个函数可以将所有可能的移动打印到一定的深度，我有一种启发式算法可以评估每一次移动，我只是不确定如何将其转换为一个返回最佳移动的函数。我只想使用Haskell库中提供的函数（不想下载任何包等）。

data Rose a = Rose a [Rose a]
    deriving Show

我想如果我画一幅图来解释我所拥有的功能，我可能会更容易理解。我有两个我能想到的解决方案，它们在图中概述了，我不确定我应该采用哪种方法，如果有的话。：

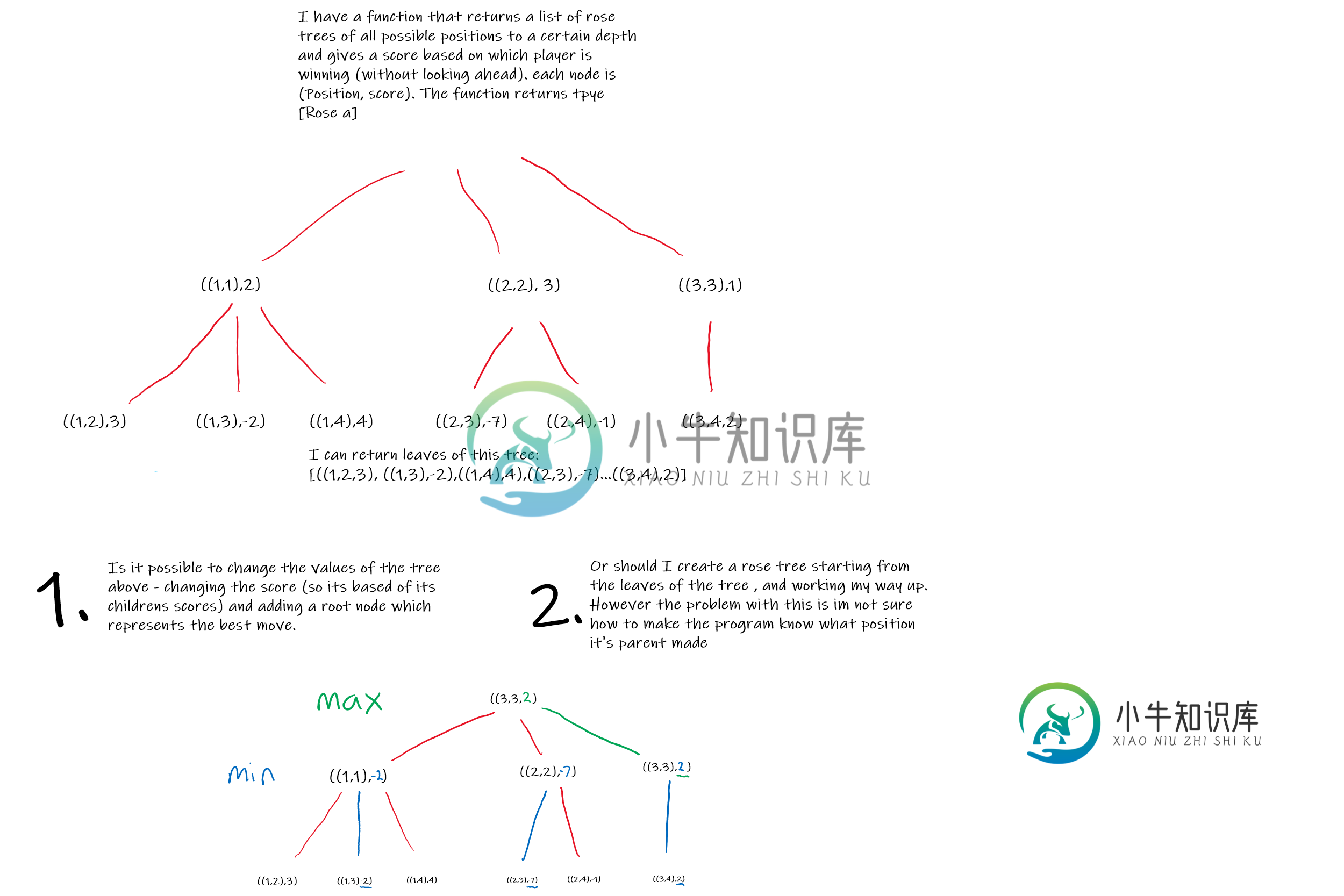
我想我需要一个函数，将图片顶部的[Rose a]转换为图片底部的Rose a。

谢谢

Answer 1

嗯，你实际上不需要建立一个更新分数的树。你只需要计算最好的移动(最大化最小的，最坏情况的分数)。

所以，从一些初步的开始：

import Data.List
import Data.Ord

type Position = (Int,Int)
type Score = Int
data Rose a = Rose a [Rose a]

我们可以编写一个函数，该函数获取移动树列表并选择移动（又名Position），从而获得最小得分的最大值：

maximin :: [Rose (Position, Score)] -> (Position, Score)
maximin = maximumBy (comparing snd) . map minscore

帮助程序min斯克尔计算移动树的最小分数，假设最佳反击。

minscore :: Rose (Position, Score) -> (Position, Score)

如果我们在一片叶子上，我们对分数的最佳估计是对当前板的直接启发式评估，所以我们只需返回该位置和分数：

minscore (Rose x []) = x

否则，我们使用最大值的反作用（即最小最大值）从最佳反击中计算分数：

minscore (Rose (pos,_) moves)
  = let (_,score) = minimax moves in (pos,score)

请注意，< code>minscore总是返回从树根开始的下一步棋(< code>pos)，但是分数将从树根(对于树叶)或通过进一步的递归计算(对于节点)获得。

最大值及其镜像minimax的完整定义为：

maximin :: [Rose (Position, Score)] -> (Position, Score)
maximin = maximumBy (comparing snd) . map minscore
  where minscore (Rose x []) = x
        minscore (Rose (pos,_) moves)
          = let (_,score) = minimax moves in (pos,score)

minimax :: [Rose (Position, Score)] -> (Position, Score)
minimax = minimumBy (comparing snd) . map maxscore
  where maxscore (Rose x []) = x
        maxscore (Rose (pos,_) moves)
          = let (_,score) = maximin moves in (pos,score)

应用于您的图片示例：

example = maximin
  [Rose ((1,1),2) [Rose ((1,2),3) [], Rose ((1,3),-2) [], Rose ((1,4),4) []],
   Rose ((2,2),3) [Rose ((2,3),-7) [], Rose ((2,4),-1) []],
   Rose ((3,3),1) [Rose ((3,4),2) []]]

你会得到：

> example
((3,3),2)

这看起来像你想要的。

关于性能的几点说明:

< Li > minimax算法实际上并不使用内部节点的启发式得分，只在叶子节点使用，因此您最好处理< code>[Rose Position]并只在需要的地方计算启发式得分(当您在< code>minscore或< code>maxscore中检测到叶子节点时)。 < li>Alpha-beta修剪是minimax算法的一种众所周知的优化，应该在任何严肃的实现中使用。

总之，完整的代码是：

import Data.List
import Data.Ord

type Position = (Int,Int)
type Score = Int
data Rose a = Rose a [Rose a]

maximin :: [Rose (Position, Score)] -> (Position, Score)
maximin = maximumBy (comparing snd) . map minscore
  where minscore (Rose x []) = x
        minscore (Rose (pos,_) moves)
          = let (_,score) = minimax moves in (pos,score)

minimax :: [Rose (Position, Score)] -> (Position, Score)
minimax = minimumBy (comparing snd) . map maxscore
  where maxscore (Rose x []) = x
        maxscore (Rose (pos,_) moves)
          = let (_,score) = maximin moves in (pos,score)

example = maximin
  [Rose ((1,1),2) [Rose ((1,2),3) [], Rose ((1,3),-2) [], Rose ((1,4),4) []],
   Rose ((2,2),3) [Rose ((2,3),-7) [], Rose ((2,4),-1) []],
   Rose ((3,3),1) [Rose ((3,4),2) []]]