理解 ROC 和 PRC
前两天看到了一篇关于 ROC 的推送文章,突然发现这块上学时的知识已经逐渐开始忘却了,顺便复习一下这部分知识顺手记录下来。
混淆矩阵
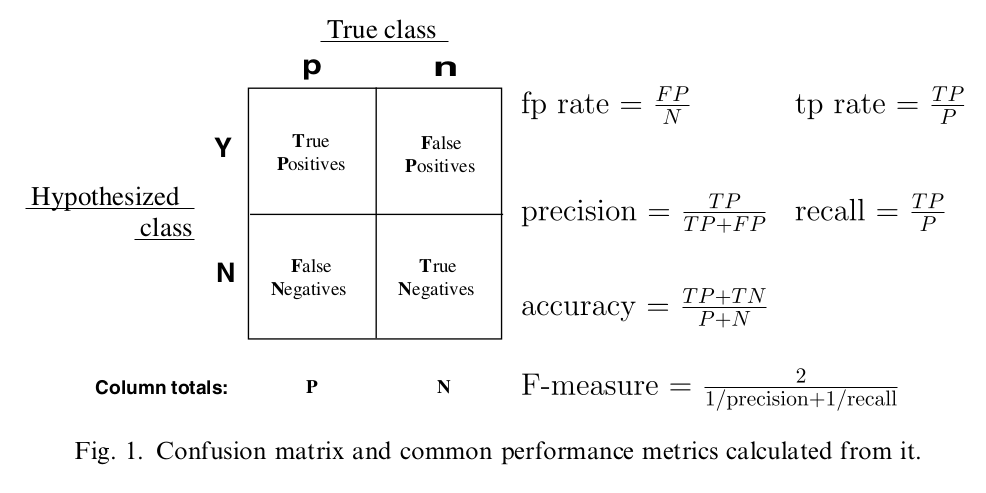
二分类问题的混淆矩阵可以衍生出 Precision 和 Recall。F1 是这两个指标的几何平均。这个指标的问题在于类别不平衡的时候,比如 99 个 A 类,1 个 B 类,分类器全部预测成 A,此时,P=0.99,R=0.99,F1=0.99,这肯定不行的对吧。
PR 曲线
PR 曲线要做的事情是对于所有的待预测 instance,计算出 positive 的概率,首先认为没有正例。
那么显然此时的 P 可以认为是 1,R 则是 0.(实际上是 P=0/0,不过我们可以暂时这么记住,初始点就是在左上角就可以。) 如下图所示。
| P | N | |
|---|---|---|
| Y | 0 | 0 |
| N | A | B |
下一步我们把 positive概率最大的判断为正例,那么势必会从 A 里面移上来一个。只要我们的模型不太拉胯,那么大概率 top1 的正例是对的,也就是说,从 A 里面移上来一个(如下图所示)。此时,P=1,R=1/A。这意味着,在 PR 图上,从初始点向右画的一小段曲线。
| P | N | |
|---|---|---|
| Y | 1 | 0 |
| N | A-1 | B |
以此类推,假设前十个我们从预测对了,都是成功的从 PN 位置把真正例移动到 YP 一格中,那么在 PR 图上就是从起始点不停向右画出了 10 个 point,最后一个点是 (P=1,R=10/A)。直到第 11 个,我们预测错了(如下图所示)。那么注意这个点是 (P=10/11,R=10/A)。相比第十个点,是 P 下降,R 不变,体现在 PR 图中就是在第十个点正下方我们画出了第十一点。
| P | N | |
|---|---|---|
| Y | 10 | 1 |
| N | A-10 | B-1 |
然后我们在看第十二个点,假设我们又预测对了(如下图所示)。则第十二个点的坐标是 P=11/12,R=11/A
| P | N | |
|---|---|---|
| Y | 11 | 1 |
| N | A-11 | B-1 |
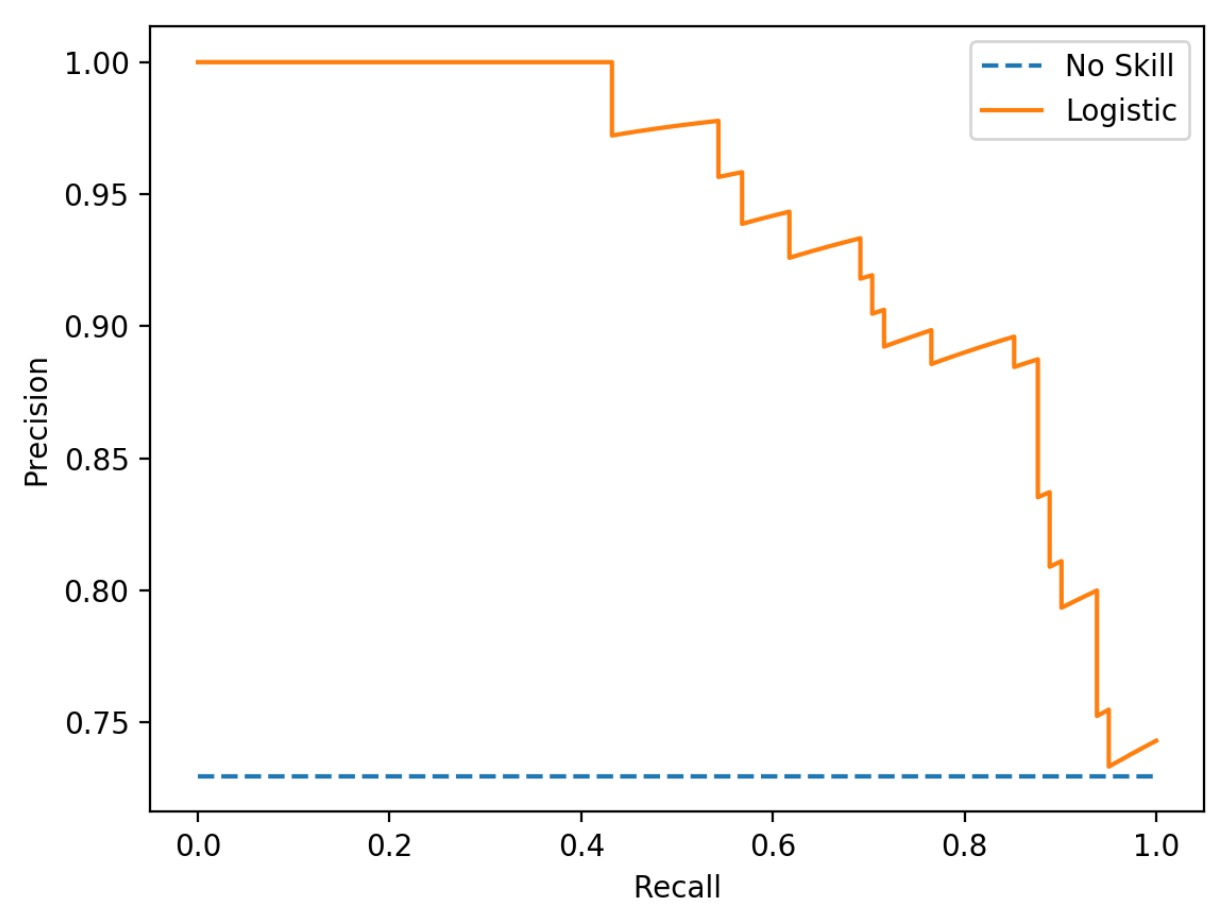
所以我们可以大概判断出来,绘制 PR 曲线的时候,预测正确一个,会向右上方画一小段曲线(除非 P=1),预测错误一个会向正下方绘制一小段曲线。比如下图是一个典型的 PR 曲线图。
我们再讨论一下最理想的场景,就是所有的最差的真正例的概率比最好的真负例的概率高。那就意味着模型的决策序列,所有的正例都被先挑出来。那 PR 曲线就会从左上角(P=1,R=0)一直向右延伸到(P=1,R=1),此时是完美的决策阈值,然后再继续(无用的)扩召回,导致曲线向下延伸到(P=0,R=1)。
决策序列:PPP…PPPPNN…NNN
我们再讨论一下随机猜测的场景,也就是差不多可以认为我们选择的序列是一个正例一个负例交替的。此时纵坐标 P 会很快的跌落到 0.5 位置处(选了两个只有一个是对的),后面就会整体水平的向右画出一根线,含义是,recall 虽然在不断提高,但是召回的部分始终只有一半是对的。
决策序列:PNPNP…NPNPNPN
AP
直觉上我们就知道,肯定计算曲线下面积是一个比较好的评估方式。AP这个指标没有 AUC 这么家喻户晓。
ROC
ROC 要做的第一步事情和 PR 曲线一样。是对于所有的待预测 instance,计算出 positive 的概率。然后以此把需改概率从高到低的 instance 决策为正例。只不过 PR 选择的两个坐标是 P 和 R,而 ROC 选择的坐标是 TPR 和 FPR。
我们还是沿用上面的例子,初始化就是下图的状态。对应的初始点是 TPR=0,FPR=0,也就是 ROC 的左下角。
| P | N | |
|---|---|---|
| Y | 0 | 0 |
| N | A | B |
然后连续十个都是预测对了正例,此时对应的数据点是 TPR=10/(A-10),这对应着从左下角的初始点水平向上画了 10 个点。
| P | N | |
|---|---|---|
| Y | 10 | 0 |
| N | A-10 | B |
然后是一个预估错误的点,这会导致 TPR 不变,但是 FPR 变大,从而向右画出一个数据点。
| P | N | |
|---|---|---|
| Y | 10 | 1 |
| N | A-10 | B-1 |
到这里我们应该就可以看出来了,每一个正确的正例选择,都会使得 TPR 上升且 FPR 不变,而一次错误的扩召回,会导致 TPR 不变而 FPR 上升。所以我们得到的曲线意一定是一个只能从左下角向上或者向右的折线。
我们再讨论一下最理想的场景,就是所有的最差的真正例的概率比最好的真负例的概率高。那就意味着模型的决策序列,所有的正例都被先挑出来。那 PR 曲线就会从左下角(TPR=0,FPR=0)一直向上延伸到(TPR=1,FPR=0),此时是完美的决策阈值,然后再继续(无用的)扩召回,导致曲线向右延伸到(TPR=1,FPR=0)。
决策序列:PPP…PPPPNN…NNN
我们再讨论一下随机猜测的场景,也就是差不多可以认为我们选择的序列是一个正例一个负例交替的。此时曲线会随机向上或者向右移动一个单位。含义是,TPR 虽然在不断提高,但是 FPR(误召回)也在不断提高。
决策序列:PNPNP…NPNPNPN
不平衡样本下 PR 和 ROC 的表现
ROC曲线有一个特性:当测试集中的正负样本分布发生变化了,ROC曲线可以保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象,即负样本比正样本多很多(或者相反),而且测试数据中的正负样本的分布也可能随着时间变化。或者召回问题中,可能正例(需要召回的 item,相比随机负例,只占 1/1000 甚至更低。)
我们这里还是伪造一个 case,假设我们有一个分类器,准确率是 80%。
那么他的预测序列可能是:
决策序列:PPPPNNPNNN
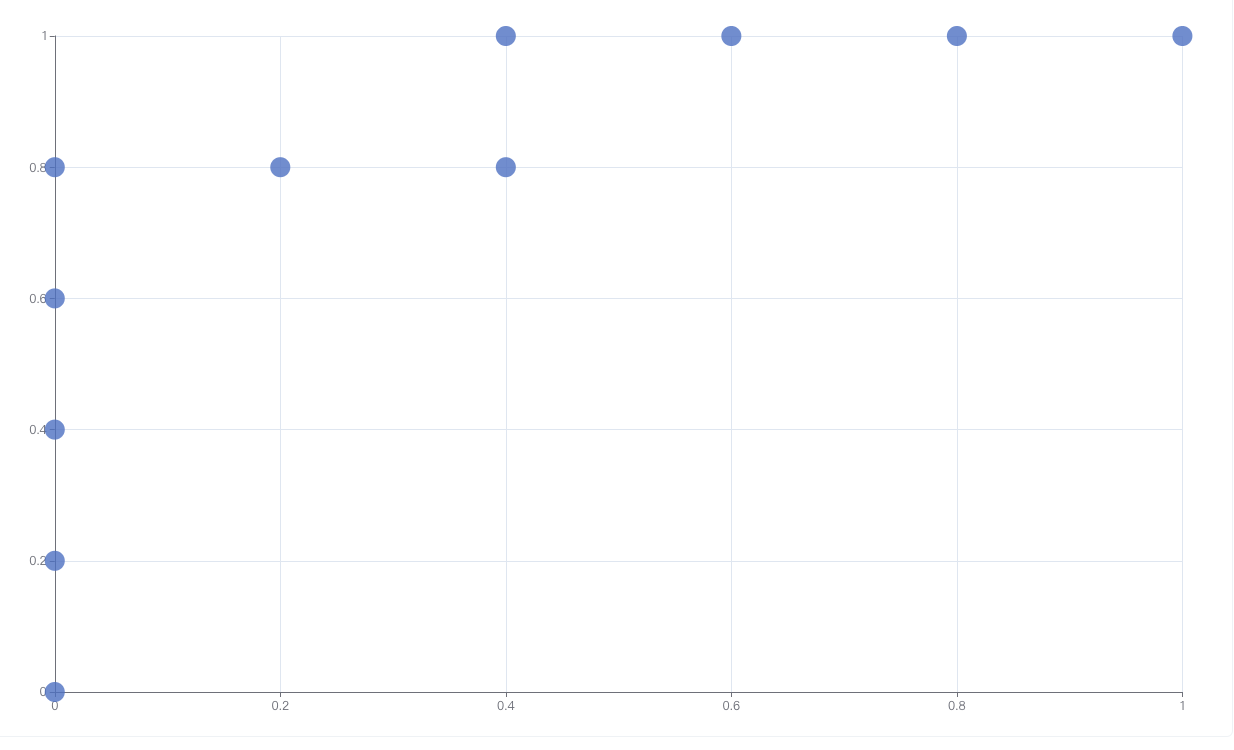
观察上面的从高到低的决策序列,如果我们 划分阈值的话,因为这是一个平衡问题,所以我们会让前 5 个输出为正例,后 5 个判断为负例,但是看字母表示的 Ground Truth 我们就会发现,有四个 instance 预测错了。
按照这个序列,我们画出 ROC,(工具不趁手,随便找一个在线工具画的)。
再画出 PRC:
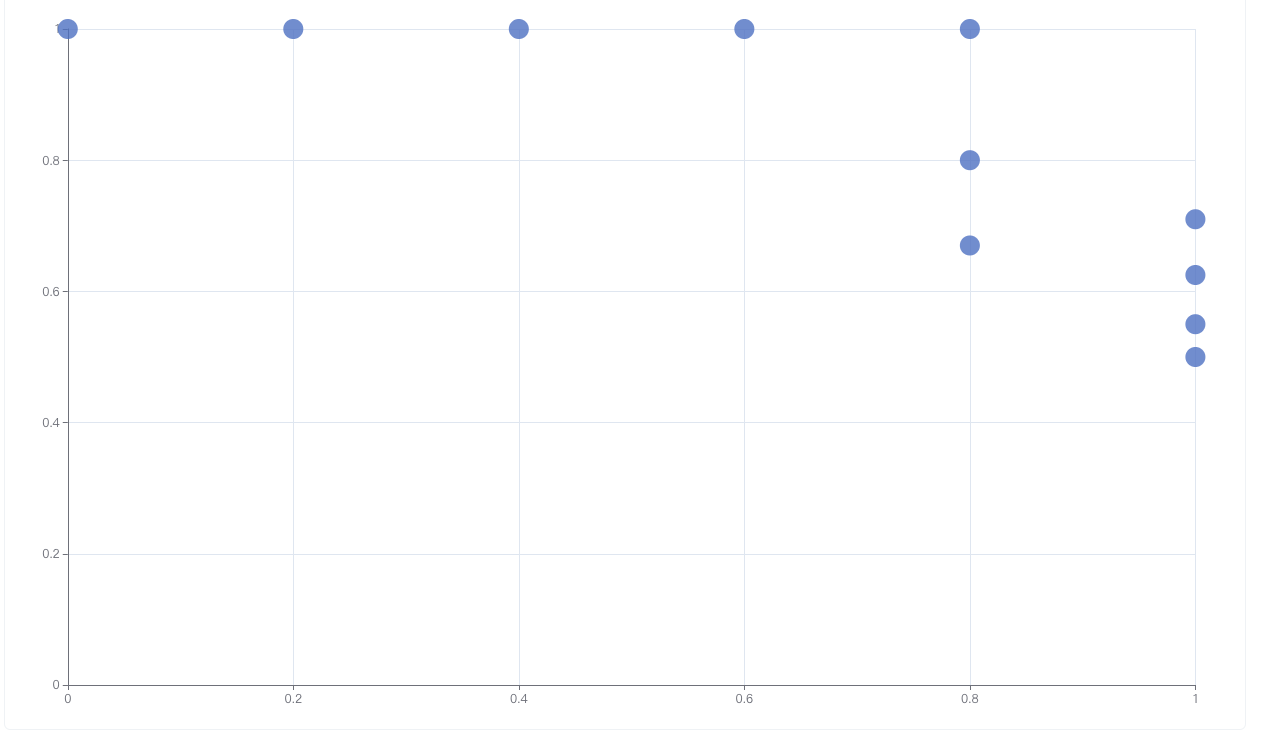
会发现,哎,看着都挺好的。
但是加入我们面对的是负例极多的召回场景,十个只有一个相关结果。
决策序列:NPNNNNNNNN
看上面的决策序列,我们知道只有一个正例,所以选择 top1 作为正例,剩下九个是负例,此时依旧有 80% 的准确率。但是这种要看场景,比如此时正在讨论的召回场景,这个80%准确率其实一点用没有,是极差的,因为我们不关心那 8 个 Neg 预测对了,我们只关心那一个 Pos 是否预测对了。
我们重新画出 ROC:
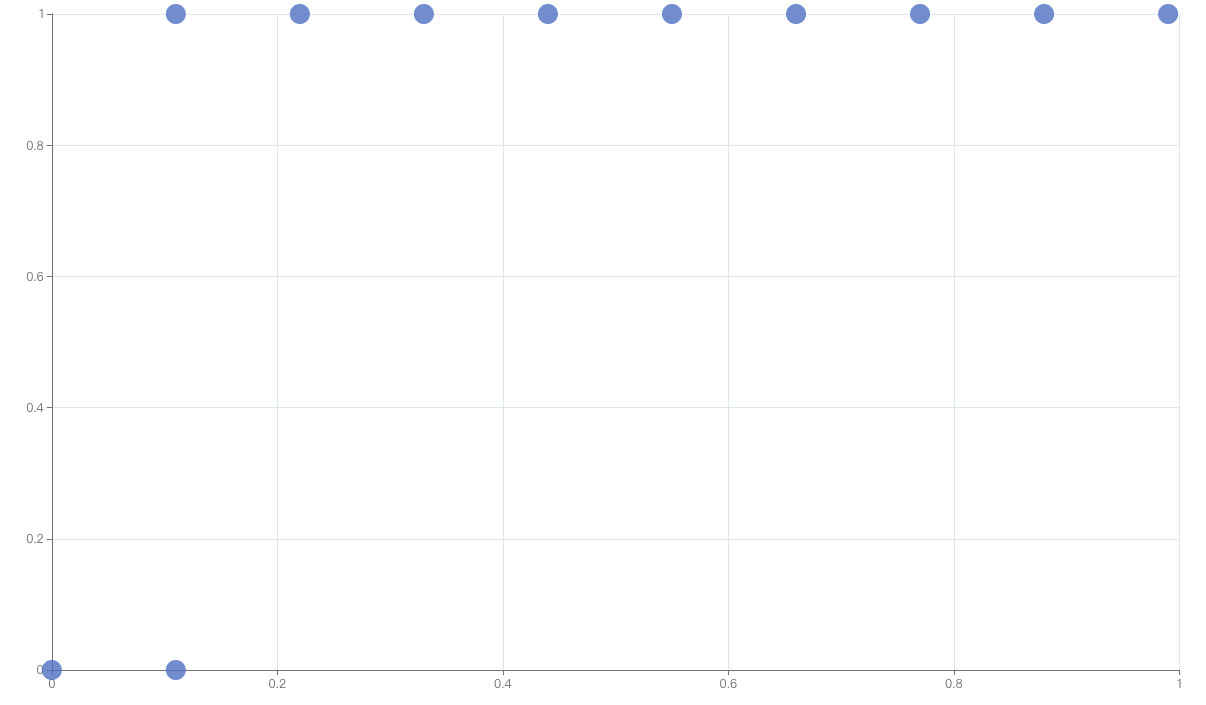
我们发现依旧看起来“相当不错”。再看看 PRC:
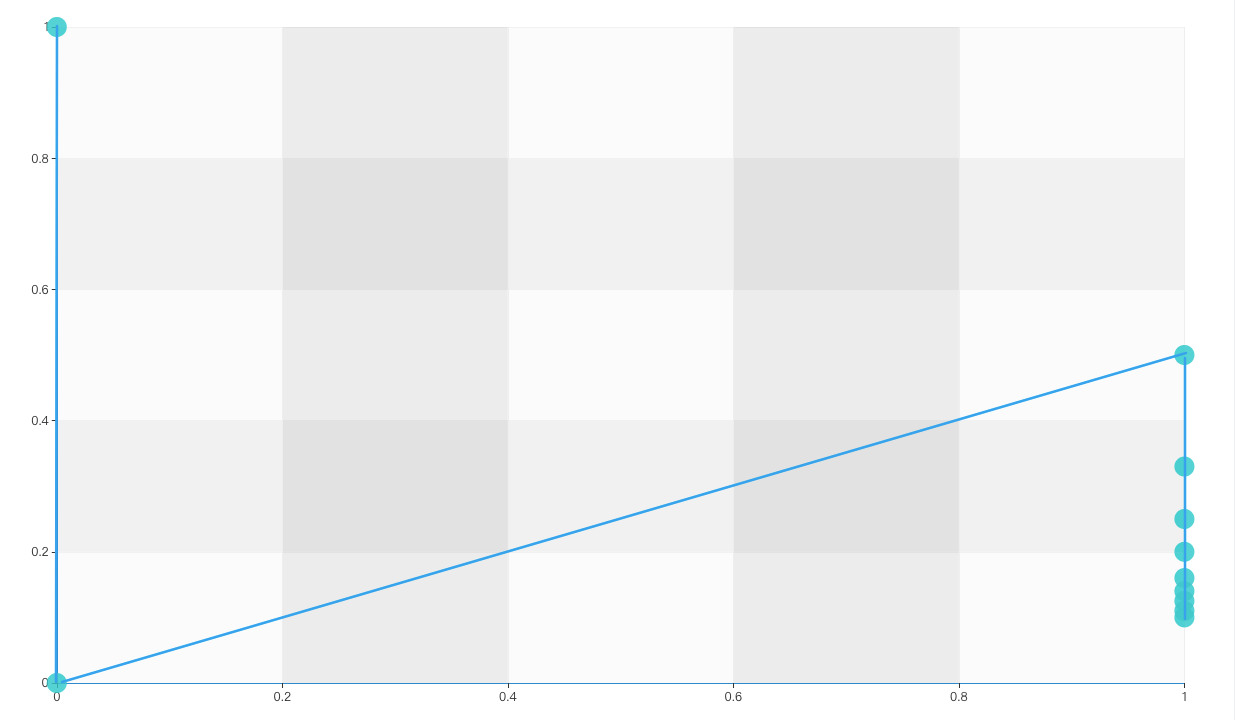
会发现 PRC 相当差,这个其实更符合我们对模型的预期。但是为什么会这样呢?
因为混淆矩阵中,不平衡问题发生在两列中,P 一列样本很少,N 一列样本很多。而 ROC 只在列内计算指标,因此两列谁多谁少他不关心。而 PRC 中的 P,关心预测为真的里面多少是真的正例,(在计算第一个点的时候,唯一一个预测为真的是伪正例,Precision=0),逻辑上更符合我们“少类敏感”的场景,数据上,这个指标是横向计算出来的,因此可以感知到两列的不敏感性。 或者说,是 PRC 更关心正例,在我们的例子中,正例就是少数类。
这也就意味着,虽然 ROC 适用于评估分类器的整体性能,但是对于类别不均衡的数据,ROC 曲线往往会过于“乐观”,因此还是 PR 曲线更好。与之相对的,PRC的情况恰恰相反,尽管召回率只在正样本基础上计算,精度准确率需要同时测量正和负样本,因此精确度的测量取决于数据中的正负之比。
ROC曲线由于兼顾正例与负例,所以适用于评估分类器的整体性能,相比而言PR曲线完全聚焦于正例。在数据分布改变后可以明显看到,ROC 曲线几乎没有改变, PR 曲线变动剧烈,时好时坏,这种时候难以进行模型比较。ROC 曲线选用的两个指标不依赖数据中具体的类别分布,因此不适合被应用于数据分布极度不均的任务中。
参考:
- An introduction to ROC analysis
- https://zhuanlan.zhihu.com/p/582869308

