对称矩阵的压缩储存讲解

一、存储矩阵用一个二维数组即可；

二、什么是对称矩阵：

设一个N*N的方阵A，A中任意元素Aij，当且仅当 Aij == Aji(0 <= i <= N-1&& 0 <= j <= N-1)，则矩阵A是对称矩阵。以矩阵的对角线为分隔，分为上三角和下三角

三、对称矩阵的压缩储存：

压缩存储称矩阵存储时只需要存储上三角/下三角的数据，所以最多存储n(n+1)/2个数据（相当于1+2+…+n,即等差数列求和）。

对称矩阵和压缩存储的对应关系：下三角存储i>=j, SymmetricMatrix[i][j] ==Array[i*(i+1)/2+j]

四、代码实现

#include<iostream>
using namespace std;
template<class T>
class CompressionMatrix
{
public:
  CompressionMatrix(T* arr,int sz)
    :_data(new T[sz*(sz+1)/2])
    ,_size(sz)
  {
    int index=0;
    //压缩储存过程
    for(int i=0;i<sz;++i)
    {
      for(int j=0;j<sz;++j)
      {
        if (i>=j)//_data中储存下三角的数据
        {
          _data[index]=arr[i*sz+j];
          index++;
        }
        else
          break;
      }
    }
  }
  //获取某个坐标的数据，i和j代表该数据在矩阵中的横纵坐标
  T GetDate(int i,int j)
  {
    if (i>=j)//下三角数据
    {
      return _data[i*(i+1)/2+j];
    }
    else//上三角数据
    {
      std::swap(i,j);//将横坐标和从坐标值交换；
      return _data[i*(i+1)/2+j];
    }
  }
    //打印矩阵的数据
  void PrintfMatrix()
  {
    for (int i=0;i<_size;++i)
    {
      for (int j=0;j<_size;++j)
      {
        cout<<GetDate(i,j)<<" ";
      }
      cout<<endl;
    }
  }
  ~CompressionMatrix()
  {
    if (_data!=NULL)
    {
      delete[] _data;
      _data=NULL;
      _size=0;
    }
  }
protected:
  T* _data;//储存数据的数组
  int _size;//储存原始对称矩阵的行数（或列数）
};

测试代码：

int main()
{
  int a[5][5]=
  {
    {0,1,2,3,4},
    {1,0,1,2,3},
    {2,1,0,1,2},
    {3,2,1,0,1},
    {4,3,2,1,0},
  };
  CompressionMatrix<int> cm((int*)a,5);//将二维数组强制转换为一维数组指针，是问题更简单
  cm.PrintfMatrix();
  return 0;
}

五、运行结果

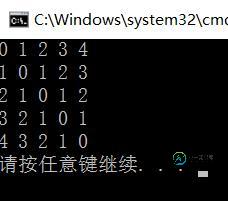
O(∩_∩)O

总结

以上就是这篇文章的全部内容了，希望本文的内容对大家的学习或者工作具有一定的参考学习价值，谢谢大家对小牛知识库的支持。如果你想了解更多相关内容请查看下面相关链接