Java矩阵连乘问题(动态规划)算法实例分析

本文实例讲述了Java矩阵连乘问题(动态规划)算法。分享给大家供大家参考，具体如下：

问题描述：给定n个矩阵：A1,A2,...,An，其中Ai与Ai+1是可乘的，i=1，2...，n-1。确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。输入数据为矩阵个数和每个矩阵规模，输出结果为计算矩阵连乘积的计算次序和最少数乘次数。

问题解析：由于矩阵乘法满足结合律，故计算矩阵的连乘积可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。若一个矩阵连乘积的计算次序完全确定，也就是说该连乘积已完全加括号，则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。

完全加括号的矩阵连乘积可递归地定义为：

（1）单个矩阵是完全加括号的；
（2）矩阵连乘积A是完全加括号的，则A可表示为2个完全加括号的矩阵连乘积B和C的乘积并加括号，即A=(BC)

例如，矩阵连乘积A1A2A3A4有5种不同的完全加括号的方式：(A1(A2(A3A4)))，(A1((A2A3)A4))，((A1A2)(A3A4))，((A1(A2A3))A4)，(((A1A2)A3)A4)。每一种完全加括号的方式对应于一个矩阵连乘积的计算次序，这决定着作乘积所需要的计算量。

看下面一个例子，计算三个矩阵连乘{A1，A2，A3}；维数分别为10*100 , 100*5 , 5*50 按此顺序计算需要的次数((A1*A2)*A3):10X100X5+10X5X50=7500次，按此顺序计算需要的次数(A1*(A2*A3)):10*5*50+10*100*50=75000次

所以问题是：如何确定运算顺序，可以使计算量达到最小化。

算法思路：

例：设要计算矩阵连乘乘积A1A2A3A4A5A6，其中各矩阵的维数分别是：

A1：30*35;     A2：35*15;     A3：15*5;     A4：5*10;     A5：10*20;     A6：20*25

递推关系：

设计算A[i:j]，1≤i≤j≤n，所需要的最少数乘次数m[i,j]，则原问题的最优值为m[1,n]。
当i=j时，A[i:j]=Ai，因此，m[i][i]=0，i=1,2,…,n
当i<j时，若A[i:j]的最优次序在Ak和Ak+1之间断开，i<=k<j,则：m[i][j]=m[i][k]+m[k+1][j]+pi-1pkpj。由于在计算是并不知道断开点k的位置，所以k还未定。不过k的位置只有j-i个可能。因此，k是这j-i个位置使计算量达到最小的那个位置。

综上，有递推关系如下：

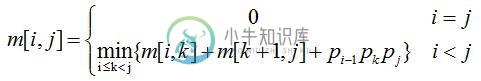
构造最优解：

若将对应m[i][j]的断开位置k记为s[i][j]，在计算出最优值m[i][j]后，可递归地由s[i][j]构造出相应的最优解。s[i][j]中的数表明，计算矩阵链A[i:j]的最佳方式应在矩阵Ak和Ak+1之间断开，即最优的加括号方式应为(A[i:k])(A[k+1:j)。因此，从s[1][n]记录的信息可知计算A[1:n]的最优加括号方式为(A[1:s[1][n]])(A[s[1][n]+1:n])，进一步递推，A[1:s[1][n]]的最优加括号方式为(A[1:s[1][s[1][n]]])(A[s[1][s[1][n]]+1:s[1][s[1][n]]])。同理可以确定A[s[1][n]+1:n]的最优加括号方式在s[s[1][n]+1][n]处断开...照此递推下去，最终可以确定A[1:n]的最优完全加括号方式，及构造出问题的一个最优解。

package Matrix;
public class Matrix {
  public static void MatrixChain(int[] p,int n, int[][] m, int[][] s) {
   for (int i = 1; i <= n; i++) {
     m[i][i] = 0;
   }
    for(int r = 2;r <= n; r++ ) {
      for(int i = 1; i <= n-r+1; i++) {
        int j = i+r-1;
        m[i][j] = m[i+1][j] + p[i-1]*p[i]*p[j];
        s[i][j] = i;
        for(int k = i+1; k < j; k++) {
          int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
          if(t < m[i][j]) {
            m[i][j] = t;
            s[i][j] = k;
          }
        }
      }
    }
  }
  public static void Traceback(int i, int j, int[][] s) {
    if(i == j) return;
    Traceback(i,s[i][j],s);
    Traceback(s[i][j] + 1,j,s);
    System.out.println("Multiply  A" + i + "," + s[i][j] + "and A" + (s[i][j] + 1) + "," + j);
  }
  public static void main(String[] args) {
    System.out.println("小牛知识库测试结果：");
    Matrix mc = new Matrix();
    int n = 7;
    int p[] = { 30, 35, 15, 5, 10, 20, 25 };
    int m[][] = new int[n][n];
    int s[][] = new int[n][n];
    int l = p.length-1;
    mc.MatrixChain(p, l,m, s);
    for (int i = 1; i < n; i++) {
      for (int j = 1; j < n; j++) {
        System.out.print(m[i][j] + "\t");
      }
      System.out.println();
    }
    System.out.println();
    for (int i = 1; i < n; i++) {
      for (int j = 1; j < n; j++) {
        System.out.print(s[i][j]+" ");
      }
      System.out.println();
    }
    mc.Traceback( 1, 6, s);
  }
}

运行结果：

更多关于java算法相关内容感兴趣的读者可查看本站专题：《Java数据结构与算法教程》、《Java操作DOM节点技巧总结》、《Java文件与目录操作技巧汇总》和《Java缓存操作技巧汇总》

希望本文所述对大家java程序设计有所帮助。